AcWing 159 奶牛矩阵 – 简略题解

AcWing 159 – 奶牛矩阵

这道题的题意让我们想起了最小循环节。我们先不考虑这个矩阵的具体位置。由题可知，只要扩展的矩阵覆盖原矩阵即可。考虑以下图形：

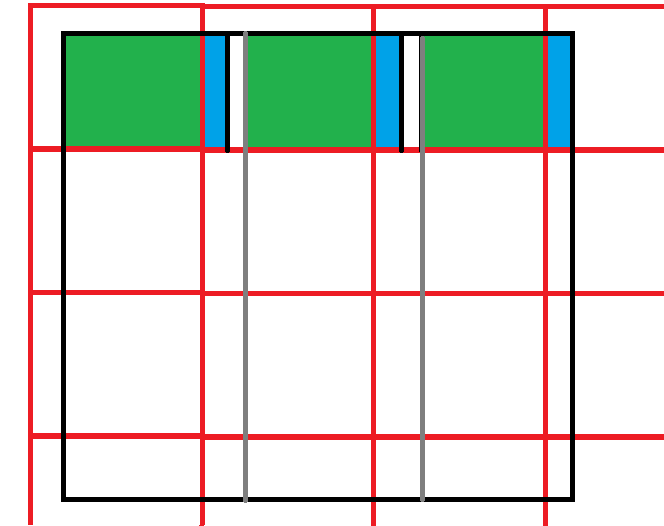
黑线为原矩阵。红线是一种最小子矩阵的划分。请看绿色和蓝色矩形，它们分别是没有占够一整个矩形宽度的左右边界，以及对应到每个完整的子矩形中的位置。如果我们以灰线为界，将最小子矩形平移至与灰线之间对齐，则最小子矩形的扩展就从原矩形的最左端开始。上下两端的处理同理。这与之前的划分显然是等价的。因此，我们可以只考虑从左端、顶端开始的子矩阵的划分。

稍加思考发现，子矩形划分的行和列互不干扰。因此我们分别处理行和列。

对于每一行，我们钦定一个靠右的位置$x$，满足将它划分为由若干个循环节构成的$S[0 \dots x]$，以及由一个不足循环节但是该循环节前缀的$S[x+1 \dots |S|-1]$构成。那么，对于一个合法的划分方案，就要求存在一个$x$，使得每一行的字串能够依照其完成上述划分。

通过$next$数组，我们可以很轻松地找到某个字符串的前缀的最小循环节。但现在我们需要找到一个未完成的循环节。考虑一个一般的$next$数据。对于$next(n-1)$，我们可以通过循环对齐的方式，复制$S[0 \dots n-next(n-1)-1]$若干次，可以拼凑出$S$的一个极长前缀，最终将余下一部分，也必定是$S[0 \dots n-next(n-1)-1]$的一部分。

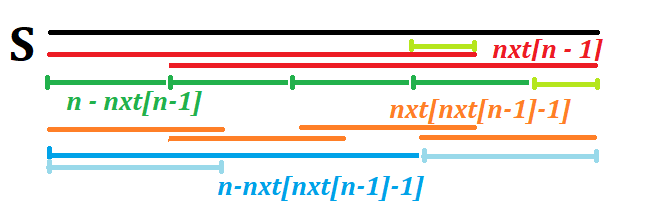
再取$next(next(n-1)-1)$，以此类推。所以，我们有可能获得的“循环节”就是$n-next(n-1), n-next(next(n-1)-1), \dots$。考虑每个求出的“循环节”，发现它的$k, k \in \mathrm{N^*}$倍也是可以完成覆盖的。于是我们记$cnt(i)$为对于行，“循环节长度可以为$i$”的字串的计数。容易发现对于所有$cnt(i)=n$，$i$是一种合法的划分。我们只要取最小的即可。同理，我们对于每一列也如此处理。

为了避免重复，我们使用bool数组或者bitset统计对于单个字串的循环节合法方案。总时间复杂度上限为$\mathrm{O}(nm+nm(\log\log n+\log\log m))$，包含了累计计数的时间。详见代码。

数据太水了……之前写过一个求各行循环节最小公倍数的错误贪心写法，竟然也能过……要不是想起来写一篇总结，可能现在都还认为那是对的……

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <bits/stdc++.h>
using namespace std;

template <typename T> inline bool read (T &x) {
	x = 0; int f = 1; char c = getchar ();
	for (; c != EOF && !isdigit (c); c = getchar ())
		if (c == '-') f = -1;
	if (c == EOF) return 0;
	for (; c != EOF && isdigit (c); c = getchar ())
		x = (x<<1) + (x<<3) + (c^48);
	x *= f; return 1;
}
template <typename T> void print (T x) {
	if (x < 0) putchar ('-'), x = -x;
	if (x > 9) print (x / 10);
	putchar ('0' + x % 10);
}
#define reint register int
#define inl inline
typedef long long ll;
typedef unsigned long long ull;
typedef __int128 lll;
typedef pair <int, int> pint;

const int N = 1E4 + 10, M = 80;
int n, m, nxt[N], x, now, minw, minh, tmp, cnt[N];
char s[N][M]; bitset <N> g;

inl void build_nxt_row (int r) {
	memset (nxt, 0, 320);
	x = 1, now = 0;
	while (x < m)
		if (s[r][x] == s[r][now]) nxt[x++] = ++now;
		else if (now) now = nxt[now - 1];
		else ++x;
}
inl void build_nxt_col (int c) {
	memset (nxt, 0, (n + 1)<<2);
	x = 1, now = 0;
	while (x < n)
		if (s[x][c] == s[now][c]) nxt[x++] = ++now;
		else if (now) now = nxt[now - 1];
		else ++x;
}

int main () {
	/*  */
	read (n), read (m); minw = minh = 1;
	for (int i = 0; i < n; ++i)
		scanf ("%s", s[i]);
	for (int i = n - 1; i >= 0; --i) {
		build_nxt_row (i);
		now = m; g.reset ();
		do {
			for (tmp = m - nxt[now - 1]; tmp <= m; tmp += m - nxt[now - 1]) g[tmp] = 1;
			now = nxt[now - 1];
		} while (now);
		for (int j = 1; j <= m; ++j) cnt[j] += g[j];
	}
	for (int i = 1; i <= m; ++i)
		if (cnt[i] == n) { minw = i; break; }
	memset (cnt, 0, sizeof cnt);
	for (int i = m - 1; i >= 0; --i) {
		build_nxt_col (i);
		now = n; g.reset ();
		do {
			for (tmp = n - nxt[now - 1]; tmp <= n; tmp += n - nxt[now - 1]) g[tmp] = 1;
			now = nxt[now - 1];
		} while (now);
		for (int j = 1; j <= n; ++j) cnt[j] += g[j];
	}
	for (int i = 1; i <= n; ++i)
		if (cnt[i] == m) { minh = i; break; }
	print (minh * minw);

	return 0;
}