CF1649F – Serious Business – 题解与思路重现
CodeForces Round #755 Div.2 F / Div.1 D Serious Business
此题整整困了我一天半,耗费了好几张草稿纸。实在走投无路,翻看题解,却发现正解曾经近在咫尺。有必要稍作整理。
考虑DP。
错误转移1
这道题与清理班次(《算法竞赛进阶指南》上的一道例题)过于相似,都是“给定一些段落,选择其中一些完整覆盖,求最小花费”的形式。记上述花费为。但本题与原题不一样之处在于其起点和终点是任意给定的。我的第一反应是枚举在位置从第行转到第行,利用数据结构维护所有,在转移到第二行,解锁到达的最小代价。对于各行前缀和,我们可以利用线段树或树状数组维护。同时我们也知道可以利用数据结构优化在的时间内,计算出对于一个固定的起点,所有的值。
但经过一上午的死缠烂打,我发现根本无法维护邻项的值。或者换句话讲,其二者甚至没有必然关联。考虑它的转移:如果存在一个段花费为,则可以更新。也就是说,我们在长度不尽相等的若干区间内取极值后作转移。然而随着发生改变,一些区间变得不再可用(右端点在左侧),而一些区间在最开始就可以被利用(其包含)。最致命的是,由于此处的最值不具有传递性,重新计算所有转移路径上的取值,还不如重新暴力求一遍呢。时间复杂度。
从上午八点到十二点半,反复确认打表后,这个朴素的DP告吹了。
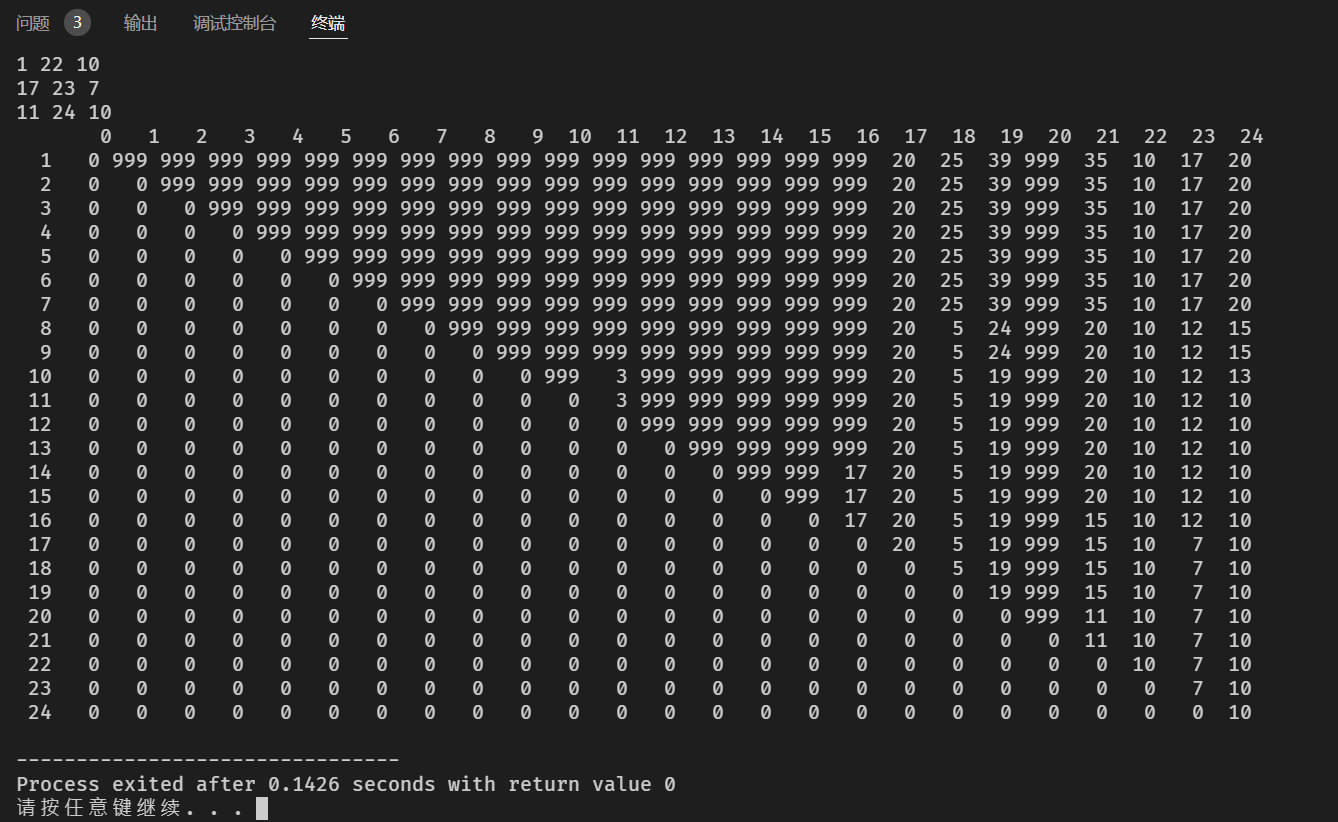
生成了一些随机的区间,从上到下分别暴力计算了到。可以发现,相邻两行之间的值难以用数据结构维护。
错误转移2
一开始做原题时,就思考过一个问题:如果我们设计的状态不包含任何关于最后选择的段落的信息,就会造成“无代价转移”或者“重复计算代价转移”。
无代价转移:考虑两个区间。有。则如果我们秉承“相同区间内解锁不重复计费”的概念,会出现的转移。
重复计算代价转移:如果我们总是在某一段不再可用()时,计入当前处在的某一段的费用,那么当实际上选择了时,转移到时还会再计算一遍。
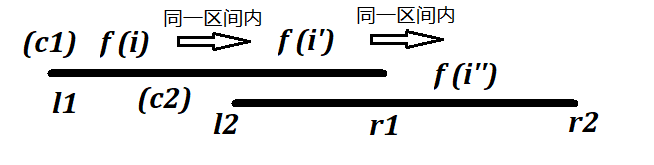
而且,我们仅仅考虑的是,不管以什么方式到达,获得的收益都最大。因此,我们没有必要关注具体是从哪个位置跳到第行,然后转移到的。
所以,不论怎么样,我们都需要——至少隐式地——记录当前最后付费区间的相关信息。一个更加朴素的DP状态已经呼之欲出了:表示从走到,同时最后付费的区间编号为的最大收益。存在以下转移:
我们发现它的转移非常奇怪,全部都只依赖。这启发我们,看它是否能通过数据结构高效维护邻项DP值。但是……对于每一个,都有不一样的参与转移,除非使用非常复杂的延迟标记系统并且在每一段的结尾处处理第一类转移(至少我是写不出来的),几乎断掉了区间修改、查询的可能性。所以,时间复杂度上限的下限是(实际上可能卡不到?!)。
整一个下午都在考虑的转移又泡汤了。
不完全正确的转移
由于我们不关心从哪里转移到第二行,同时还要确保每一段的费用被合理计算,那干脆……先放弃掉在每一段内部的转移,也即只考虑到达每一段结尾时分数最大值,继续改造原题的DP。
设表示到达时积累的最多分数。其中,。由于这是每一段的末尾,转移就具有了唯一性。存在以下转移:
至少我们写出来了。通俗的说,我们可以从该段内部利用前序状态,加上从某一段结尾到该段结尾的所有分数;或者在该段中的某一位置从第行跳下来。两种方式都不重不漏地计算了到该段末尾需要计入该段费用的所有方案。时间复杂度。
但想必上式中间的一坨前缀和的维护已经够麻烦了,还要处理一个棘手的问题:现在只能从每一段的末尾转移到第三段去,那段落中央的又如何计算?一筹莫展。
完全不正确的转移
昨天深夜脑子抽风,又跑去把在上文中枪毙的状态(表示不知晓最后付费的具体区间时到达的最大收益)推导了好几遍。
正解
考虑刚刚的转移。假如我们代码能力足够强,真的稳健地维护了前缀和及其极值,然后成功计算了那一堆复杂的取极值的式子,它唯一的毛病在于:不包含从某一段中间转移到第行的方案。有没有办法单独计算呢?
在此之前,先要对我们上文的式子做一些简化。记,则对于某一种方案,在处转移到第行,处转移到第行,其收益为:,其中表示将全部解锁的最小代价——这正是我们在错误转移1中尝试直接维护但宣告失败的东西。但可以肯定,只要固定,最终收益必然包含;但凡我们决定在处切入第行,最终收益必然包含
现在,假若我们要重写一遍上述式子,那就方便多了:
考虑某个具体的方案,它一定至少解锁了一个段落才得以跳转到第行。那么考虑它倒数第二个解锁的段落为,最后解锁的段落为,,显然该方案应该走完了——否则不必解锁段落。那么,它的最终代价就是。固定最终段落,那么问题就转变成了求。再来考虑只解锁一个段落的情况,即可转化为
我们惊奇地发现,函数是常量;在计算之前就已经更新完成,无后效性。它可以在线段树上分治求解!更具体地,我们保存每个区间内部的这些式子的答案。对于两个相邻区间的并,直接由定义计算符合相应位置关系的最值,并更新最终答案即可。
至此,本题终于告一段落。它检验了对前缀和优化区间求和、DP转移的无后效性和状态的最优性、线段树上分治这些重要技巧的灵活运用——而我并没有悉数掌握。这就是综合题“每个算法和技巧都很普通,组合到一起却没法把控”的精妙吧。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
#include <bits/stdc++.h> using namespace std; template <typename T> inline bool read (T &x) { x = 0; int f = 1; char c = getchar (); for (; c != EOF && !isdigit (c); c = getchar ()) if (c == '-') f = -1; if (c == EOF) return 0; for (; c != EOF && isdigit (c); c = getchar ()) x = (x<<1) + (x<<3) + (c^48); x *= f; return 1; } template <typename T, typename... Targs> inline bool read (T &x, Targs&... args) { return read (x) && read (args...); } template <typename T> void print (T x) { if (x < 0) putchar ('-'), x = -x; if (x > 9) print (x / 10); putchar ('0' + x % 10); } template <typename T, typename... Targs> inline void print (T x, Targs... args) { print (x), putchar (' '), print (args...); } #define reint register int #define inl inline #define newl putchar('\n') typedef long long ll; typedef unsigned long long ull; // typedef __int128 lll; // typedef long double llf; typedef pair <int, int> pint; constexpr int N = 5e5 + 10; constexpr ll INF = LLONG_MAX>>2; int n, m, a[3][N], l, r, c; ll pre[3][N], pc[2][N], ans = -INF, f; struct offer { int l, r, c; bool operator < (const offer &b) const { return r < b.r; } } g[N]; template <typename T> inl void gomx (T &x, T y) { x = max (x, y); } struct seg_tree { struct info { ll f, p[2], psum, fsum; } const INULL { -INF, {-INF, -INF}, -INF, -INF }; struct node { info dta; int l, r; } t[N<<2]; inl info select (info &a, info &b) { return { max (a.f, b.f), { max (a.p[0], b.p[0]), max (a.p[1], b.p[1]) }, max (max (a.psum, b.psum), a.p[0] + b.p[1]), max (max (a.fsum, b.fsum), a.f + b.p[1]) }; } #define post(x) (t[x].dta = select (t[x<<1].dta, t[x<<1|1].dta)) void build (int x, int l, int r) { t[x] = { INULL, l, r }; if (l == r) { t[x].dta = { -INF, { pc[0][l], pc[1][l] }, pc[0][l] + pc[1][l], -INF }; return; } int mid = l + r >> 1; build (x<<1, l, mid); build (x<<1|1, mid + 1, r); post (x); } void upd_f (int x, int tar, ll _f) { if (t[x].l == t[x].r) { gomx (t[x].dta.f, _f); gomx (t[x].dta.fsum, t[x].dta.p[1] + _f); return; } int mid = t[x].l + t[x].r >> 1; upd_f (tar <= mid ? x<<1 : x<<1|1, tar, _f); post (x); } info query (int x, int L, int R) { if (t[x].l >= L && t[x].r <= R) return t[x].dta; int mid = t[x].l + t[x].r >> 1; info lres = INULL, rres = INULL; if (L <= mid) lres = query (x<<1, L, R); if (R > mid) rres = query (x<<1|1, L, R); return select (lres, rres); } #undef post } seg; seg_tree::info res; int main () { /* CF1649F - Serious Business 吴秋实 */ read (n, m); for (int i = 0; i < 3; ++i) for (int j = 1; j <= n; ++j) read (a[i][j]), pre[i][j] = pre[i][j - 1] + a[i][j]; pc[0][0] = pc[0][1] = -INF; for (int i = 1; i <= n; ++i) pc[0][i] = pre[0][i] - pre[1][i - 1], pc[1][i] = pre[2][n] + pre[1][i] - pre[2][i - 1]; seg.build (1, 0, n); for (int i = 1; i <= m; ++i) read (g[i].l, g[i].r, g[i].c); sort (g + 1, g + m + 1); // 右端点递增排序。 for (int i = 1; i <= m; ++i) { res = seg.query (1, l = g[i].l, r = g[i].r); gomx (ans, res.psum - (c = g[i].c)); // 只采用一段的计费。 f = res.p[0] - c; // (直接从段内转移下来的)更新dp值。 res = seg.query (1, l - 1, r); gomx (ans, res.fsum - c); // 前序转移而来的计费。 res = seg.query (1, l - 1, r - 1); gomx (f, res.f - c); // 更新dp值。 seg.upd_f (1, r, f); } print (ans); return 0; }
