恕我语文不好,实在不晓得用何种词汇来描述看到下文的感受:
此比赛为正常的提高组难度,
甚至可以用来作为普及组模拟赛。 请选手 AK 后不要大声喧哗,以免影响他人 AK。
尤其是这套题的出题人是张隽铠的情况下。当然,OI 圈风气本就如此,我也不好过多评价。No comment.
T1 还算顺利,半小时左右搞定。T2 是大分类讨论,足够恶心人,但好在有相当可观的可以通过暴力与观察拿到的部分分。T3 猜测与线性基相关,但没有相应知识储备,暴力跑路。
T4 就……反正出题人开心就好。到现在都没人改出来。
一句话题解
A – 序列
依次往某个子序列中添加元素。则添加的元素必然成为新的最大值/最小值之一,否则违背题意。
于是枚举子序列首元素,将以其开头的严格上升子序列数与严格下降子序列数相乘即可。使用树状数组转移即可。复杂度 。
B – 最段路
做法
依次枚举起点为 暴力 BFS,可以通过 及 的数据,需作常数优化(评测时也别开多线程)。
打表观察 时答案的性质,可以获得另外一部分分数。
正解
我们还是考虑在网格图上移动。不过代价分 种:
- 在相邻的两个网格点之间移动,权值为 ;
- 在某个网格点旋转 ,权值为 ;
- 按当前方向通过网格点,权值为 。
自然地,我们尽可能利用前两种边到达终点,尽可能不直接通过网格点。例如,当 时,我们最多可以造成 次转向。
实际情况可以分为:
- 从 出发,抵达 (右侧出发上方到达);
- 从 出发,抵达 (右侧出发左侧到达);
- 从 出发,抵达 (下方出发上方到达);
- 从 出发,抵达 (下方出发左侧到达)。
上述四种可以化归为两种,分别计算钦定出发/到达方向后的最段路长度和路径数。但仍需分别考虑 ,以及 时的特殊情况,非常繁琐。
C – 集合
线性空间 – OI-Wiki
高斯消元 – OI-Wiki
对矩阵进行初等行变换,行空间(所有行向量张成的线性空间)不改变。列亦然。
Hamel 基 – OI-Wiki
将 个 维向量排成 的矩阵,作高斯消元消成上三角矩阵,表出的线性空间不变,所有非 ( 元)向量构成该线性空间的一个 Hamel 基。
不论开始初等行变换时选择哪些元素作为主元,对于一组确定的向量,其张成的线性空间仍保持不变。
正因如此,在异或线性空间中, 个二进制数(均为长为 的 01 向量)相互异或能表示出的所有数(张成的线性空间),可以在 的时间内求出其线性基(作行初等变换)。我们依次考虑向量的第 维(二进制表示下的第 位),选择一个该维非 的向量作为主元,消去其他所有向量的这一维,最终会得到一个每一维至多只有 个行向量不为 的线性基(二进制最高位互不相同)。
那么,通过贪心/二进制拆分等技巧,可以在 的时间内求出该线性空间的最大/第 大元素、查询某向量能否被该基表出,同时借此支持元素的动态插入/删除。
正解
考虑一个方案的最终权值为 。我们将其视作平面直角坐标系中一点 ,则所有方案构成的点集中,显然只有下凸壳上的点可能成为最优解。
解一 – 迭代求取实际凸壳
洛谷题库 P5540 最小乘积生成树 和该解法关联密切。通过贪心,找到最接近 轴的两个点 ,是为只考虑 或 最小化时的方案。我们找一点 ,使得他与 能构成下凸壳,且 最大( 离 的距离最大)。考虑 ,有只与 的线性相关项,可以将二维权值转化为一维,排序后贪心求解即可求出 。分别对 , 作上述迭代即可。
至于复杂度……李天游说决策点实际上有 (还是 ?)个,在 时由 个点构成的点集的凸壳上点数期望是 级别的。实际上该解法跑得很快(因为难以构造高强度数据)。
解二 – 利用必要非充分条件——反比例函数切线截矩
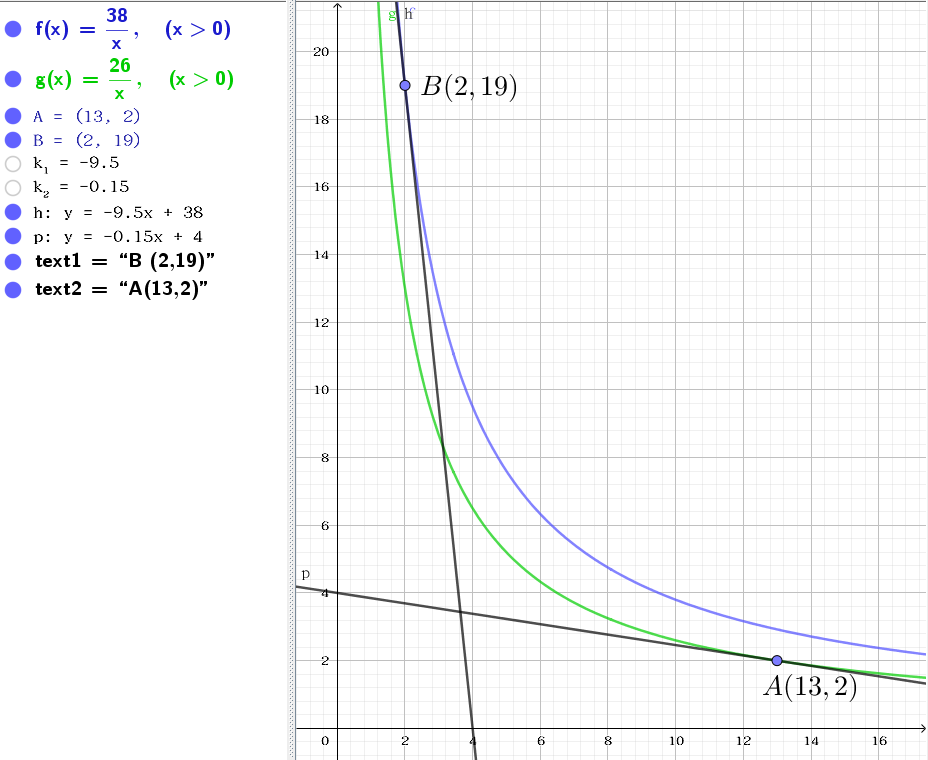
如图。显然 最优,但 亦在 构造的反比例函数切线上方。
若 成为最优解,则考虑经过它的直线 ,其中 ,是为反比例函数 在 处的导数之相反数;。则显然地,所有其他决策点都应在该直线上方。换句话说,过每个点作斜率为 的直线,最优解所在点的截矩 最小;反之则不一定成立。这是该点成为最优解的必要非充分条件。
考虑一个固定的 。对于一点 ,其截矩为 ;同时,若权值是一维且具有偏序关系,很容易排序后贪心求取一组向量的权值最大/最小线性基。所以我们直接考虑每个元素的一维权值为 ,排序后依次尝试加入线性基,(对于所有可能的 )最终得到的答案将一定包含最优解。
若把 看作自变量, 分别作斜率和截矩,则 条一次函数的交点是 级别的。所以我们求出使得相对大小改变的所有 ,从小到大依次考虑决策集合,就会有“互换两个序列中相邻元素后重新贪心求取整个序列的线性基”的需求。我们不必遍历整个序列——由 可知,序列前缀张成的线性空间不变,故尝试取出并重新将这两个元素加入线性基是正确的。
时间复杂度 。
D – 字符串
待补。
