MOCK NOIP 20221110 日志

fread 专场。$4$ 道题里面 $3$ 道适合用快读。

简略题解

A – 远征

由题意可得 $a_i$ 应为目前战斗力 $x$ 的子集。这一迭代过程最多只有 $10$ 轮（$a_i,x\leq 1023=2^{10}-1$），于是处理出跳转指针暴力模拟即可。

复杂度 $\newcommand\bigO{\operatorname{O}}\bigO(1024n)$。

B – 传送

观察样例可以感知到答案应当只有 $-1,0,1,2$ 四种取值。

根据题意，在原图 $G$ 上若有一条简单路径（在迭代加边的过程中绕回原点不符和要求） $x\rightarrow\cdots\rightarrow y$，满足其长度 $l\equiv 1\pmod{2}$，那么 $G’$ 上一定存在边 $(x,y)$。

所以若 $x,y$ 不在同一连通块中，无解；若存在满足题意的路径，答案即为 $1$；否则必须经某个点中转，答案为 $2$。

考虑图 $G$ 的任意一棵 DFS 树。将这棵树作二分图染色，若 $x,y$ 异色，则答案自然为 $1$；否则需要通过奇数条非树边，且这条非树边 $(u,v)$ 需要满足 $u,v$ 同色，才能使得该询问答案是 $1$。有一常用性质为无向图的 DFS 树没有横叉边，则为了构成一条简单路径，必须满足经过的返祖边所连接的祖先在当前节点 $x$ 的子树以外。则我们统计 $x$ 的子树内是否存在这样的返祖边（同时要满足连接的两点同色），记作 $b_x\in\{0,1\}$。记在原树上从 $x$ 到 $y$ 的简单路径上的点为 $u_1,\cdots,u_k$。如果 $b_{u_i}=1$ 且 $u_i\neq \operatorname{lca}(x,y)$，则该查询答案为 $1$。

复杂度 $\bigO(n)$，常数极大。

C – 矩阵博弈

我们发现同一行里面的所有石子互不区分。于是将题目中的游戏转述为：

给定非负整数 $c_1,c_2,\cdots,c_n$，两人轮流操作。每次均应选择 $\{1,\cdots,n\}$ 的一个非空子集 $S$，满足 $\forall i \in S, c_i>0$。然后令 $\forall i\in S,c_{i}\leftarrow c_i-1$。不能操作的人判负。

打表可以发现，先手必败当且仅当 $\forall i \in \{1,\cdots,n\}, 2\mid c_i$。这也是容易证明的：若一开始石子数全为偶，则后手可以选取与先手完全相同的操作集合使得后手操作完成后石子数仍然全为偶。石子数有限，故在偶数轮以后必定递归到全为 $0$ 的必败态。

于是题意变为：统计所有“存在至少一行，该行的所有元素之和为奇数”的子矩阵数量。我们用子矩阵总数减去“该子矩阵所有行的行内元素之和为偶数”的数量即可。

记 $\newcommand\pre{\operatorname{pre}}\pre(i,j)=(\sum_{k=1}^{j}a_{i,k})\bmod{2}$。则若以 $(x,y)$ 为左上角，$(p,q)$ 为右下角的子矩阵满足条件，必然有 $\pre(i,y-1)=\pre(i,q),\forall x\leq i\leq p$。

$\text{52 pts}$ 做法

从上到下考虑每一行。令第 $x$ 行为统计的子矩阵的最后一行。则枚举 $y,q$（子矩阵左右边界），维护 $f(y,q)$ 表示以 $x$ 行为底端、$y,q$ 为左右边界时，有 $\forall x\geq i>x-f(p,q), \pre(i,y-1)=\pre(i,q)\land \pre(x-f(y,q),y-1)\neq\pre(x-f(y,q),q)$（即，在该左右边界下的最高子矩阵）。答案减去加上所有转移后的 $f(y,q)$ 即可。

复杂度 $\bigO(nm^2)$。

$\text{72 pts}$ 做法

记 $S(y,x)$ 表示由 $\pre(1,y),\pre(2,y),\cdots,\pre(x,y)$ 依次拼接而成的 0-1 串。

钦定子矩阵上边界 $x$，枚举下边界 $q$。用字符串哈希（需要基本上 strongly-universal——字符集只有 $\{0,1\}$ 且所有串等长，设计不好极容易发生碰撞）维护每个 $S(y,q)$ 的从第 $x$ 个位置开始的后缀（我们钦定了上边界），用桶容器存储相同哈希值计数，逐行添加字符并重新计算哈希值即可。复杂度为大常数 $\bigO(n^2m)$，需要手写高效的哈希表。

正解

实际上我们统计的，就是$$\sum_{x=1}^{n}\sum_{y=0}^{m-1}\sum_{q=y+1}^{m}\newcommand\lcp{\operatorname{lcp}}\lcp(S(y,x),S(q,x))$$

每一次从第 $x$ 行向下移动一行，都有 $S(i,x+1)=\mathtt{0,1}+S(i,x)$。这个“每次向字符串开头添加一个字符”的过程像极了……（倍增法）后缀数组的构建过程。不过这不是同一个串的不同后缀，而是若干个等长的串。

记 $\newcommand\rank{\operatorname{rank}}\rank(x,i)$ 表示将 $S(0,x),S(1,x),\cdots,S(m,x)$ 字典序升序排序后 $S(i,x)$ 的排名（相等串顺序任意），$\newcommand\sa{\operatorname{sa}}\sa(x,i)$ 表示排序后排名第 $i$（0-indexed）的串的编号，$\newcommand\height{\operatorname{height}}(x,i)$ 表示排序完成后排名第 $i$ 和第 $i-1$ 的串的最长公共前缀。和后缀数组一样，容易通过单调栈记录后缀最小值的方式，利用 $\height$ 计算出所有 $S(i,x)$ 两两间 $\lcp$ 的长度。从第 $x$ 行转移到 $x+1$ 行也很简单：我们在所有串的最前面添加了一个 $0$ 或者 $1$。对于 $\sa$，类似归并排序的逆过程，将所有 $\pre(x+1,i)=0$ 的 $i$ 依原来的排序放在前边，剩下的放在后边，然后 $\bigO(m)$ 计算新的 $\height,\rank$ 即可。

时间复杂度 $\bigO(nm)$。

D – 超现实树

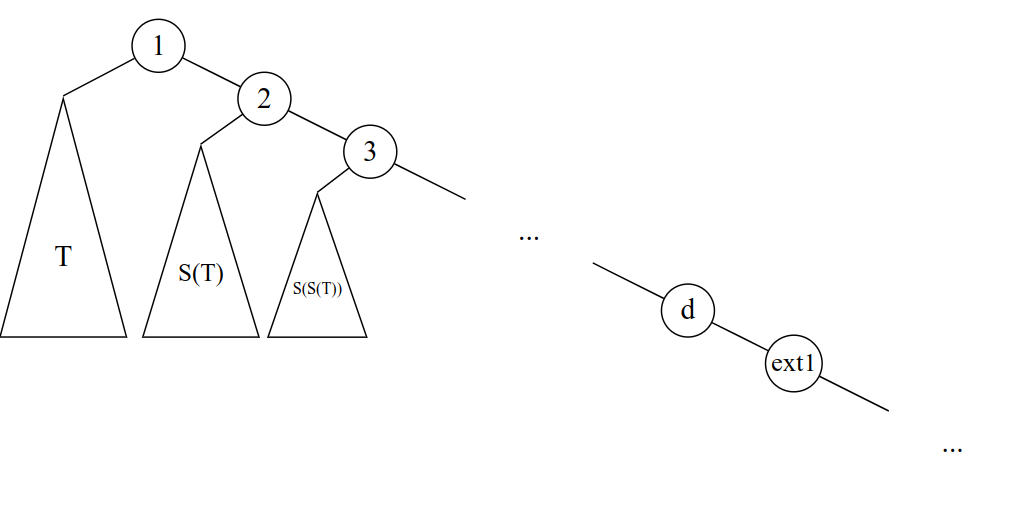图示为一棵合法的超现实树。记左树为 $T$，记一棵树 $T$ 的修剪（去除叶子结点）为 $S(T)$，则根据题意可得，根节点右儿子的左树为 $S(T)$，右儿子右儿子的左树为 $S(S(T))$……以此类推。直到最后有 $S^{d-1}(T)$ 为空时，我们可以添加任意长度的右链，这仍然是一棵超现实树。可以说，若不考虑添加的右链（图示的 $\text{ext}$ 系列节点），$T$ 能够唯一确定这棵超现实树的形态。

（形象的解释：我们把整棵超现实树的叶子砍掉，能够使得它向右儿子“滑动”一个位置而跟原位置匹配。）

题目要求统计的超现实树有以下限制：叶子数 $n$，大小 $m$ 以及深度 $k$。记 $\newcommand\siz{\operatorname{siz}}\siz(T)$ 为 $T$ 的大小，$\newcommand\dep{\operatorname{dep}}\dep(T)$ 为 $T$ 的深度，$\dep(x)$ 为以 $x$ 为根的子树深度，$\newcommand\leaf{\operatorname{leaf}}\leaf(T)$ 为 $T$ 的叶子个数。

记整棵（不计算右链的）超现实树为 $Q$。则有 $$\begin{aligned} &\dep(Q)=\dep(T)+1\\ &\siz(Q)=\sum_{x \text{\space in tree\space} T}\dep(x)+\dep(T)+1\\ &\leaf(Q)=\siz(T)+1 \end{aligned}$$

于是我们需要设计一种能够将一棵树 $T$ 唯一映射到一种类别——或者说，唯一一种生成方式的计数方法，以不重不漏地统计所有满足条件的 $T$ 的个数。当我们不断裁剪一棵树时，我们不断删除所有能删的叶子结点。如果考虑其逆过程，则对于树 $T$ 的所有叶子，它在下一轮（对应裁剪的“上一轮”）中必定存在至少一个儿子节点。于是我们可以唯一地“扩展”出树 $T$：我们让节点 $x$ 在扩展的倒数第 $\dep(x)$ 层成为其父亲的儿子，并在接下来的一轮中，它将至少添加一个儿子，而它自身将不再是叶子结点。

记 $f(d,s,l,p)$ 为“深度为 $d$、大小为 $s$、目前有 $l$ 个暴露的叶子结点、且 $\sum_{x \text{\space in tree\space} T}\dep(x)+\dep(T)+1=p$”的所有 $T$ 的数量之和。转移则是考虑添加新的 $c$ 个叶子结点。由上述过程可知，我们应保证所有 $l$ 个节点至少有了一个儿子；同时，剩余的其他节点将作为目前不是叶子结点的儿子。容易发现，无论一棵大小为 $s$ 的二叉树形态为何，总是有 $s+1$ 个位置能够添加儿子。衍生出子问题 $g(s,l,c)$：有 $s$ 件不同物品，其中 $2l$ 件物品每两个分成一组（剩余的 $s-2l$ 件独立存在），选取其中的 $c$ 件物品，满足 $l$ 组中每一组都有至少一件物品选中的方案数。这可以用容斥原理简单计算。

当我们添加了 $c$ 个儿子且保证当前叶子结点均有后继时，所有节点 $x$ 的 $\dep(x)\leftarrow \dep(x)+1$。则有转移 $$f(d+1,s+c,c,l+s+c)\leftarrow f(d,s,l,p)g(s+1,l,c)$$

上述 DP 的状态数没有看起来那样多：可以由树 $Q$ 的形态发现，当 $d\geq 20$ 时，$\siz(T)>180$；而 $s\leq n\leq 50$；$l$ 不应超过 $s$，同时如果发生转移，$l+s\leq n$。故而 $l\leq 25$。总状态数约为 $20\times 50\times 25\times 180$，总转移次数约为前者与 $25$ 之积，可以通过。