NOIP 2022 T4 – 比赛 (match) – 题解

洛谷题库 P8868 [NOIP2022] 比赛

本文记号可能稍显凌乱，但都能在题面或者前文中找到定义。

部分分

$\text{20 pts}$ – $n,Q\leq 3000$

考虑枚举所有 $\newcommand\bigO{\operatorname{O}}\bigO(n^2)$ 个区间，预先计算它们本身的答案。记 $$\begin{aligned}g_a(l,r)&=\begin{cases}\max\{a_i\mid l\leq i\leq r\},&(1\leq l\leq r\leq n)\\0&\text{otherwise}\end{cases}\\g_b(l,r)&=\begin{cases}\max\{b_i\mid l\leq i\leq r\},&(1\leq l\leq r\leq n)\\0&\text{otherwise}\end{cases}\end{aligned}$$ 则做前缀和 $s(l,r)=\sum_{i=l}^{r}g_a(l,i)g_b(l,i)$，对于询问 $[\text{ql},\text{qr}]$ 只需回答 $\sum_{i=\text{ql}}^{\text{qr}}s(i,\text{qr})$ 即可。

令 $n, Q$ 同阶，时空复杂度 $\bigO(n^2)$。

$\text{32 pts}$ – $n\leq 2.5\times 10^5, Q\leq 5$

思考单独计算每个询问的答案。

设 $\newcommand\lbd{\operatorname{lbd}}\newcommand\rbd{\operatorname{rbd}}\lbd(i)$ 满足 $(\lbd(i)=1\lor a_{\lbd(i)-1}>a_i)\land \max\{a_j\mid \lbd(i)\leq j<i\}<a_i$，也即 $g_a(l,r)=\max\{a_j\mid l\leq j\leq r\}=a_i$，应满足 $\lbd(i)\leq l\leq i$；$\rbd(i)$ 同理。它们可以由前后两遍单调栈 $\bigO(n)$ 求出。

对于询问 $[\text{ql},\text{qr}]$，从 $a$ 的角度出发考虑贡献。记 $$f_b(p,i,j,q)=\sum_{l=p}^{i}\sum_{r=j}^{q} g_b(l,r)\quad(p\leq i\land j\leq q)$$若对于所有 $i\in[\text{ql},\text{qr}]$，我们能求出 $f_b(\max(\lbd(i),\text{ql}),i,i,\min(\rbd(i),\text{qr}))$，那么将其乘上 $a_i$ 累加到答案中。

设想一个矩阵 $\mathbf{B}$，有 $\mathbf{B}_{l,r}=g_b(l,r)$，则现在我们有 $\text{qr}-\text{ql}+1$ 个上述询问，要求出矩阵区域和。

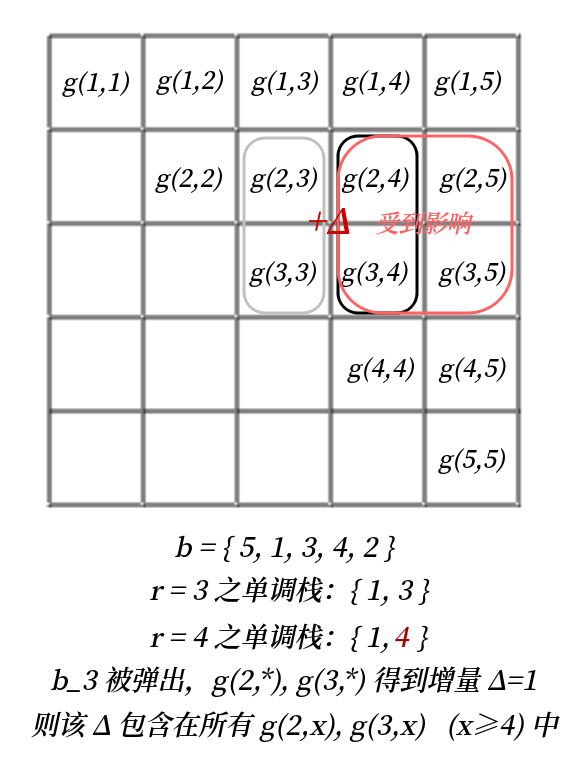如果我们只计算一列中连续几行元素的和，它是一个经典扫描线问题：借助单调栈和区间加线段树，我们能轻松维护“在 $r$ 分别为 $1,2,\cdots,n$ 时，任意 $l\ (l\leq r)$ 的 $g_b(l,r)$”。更具体地，我们维护一个 $b$ 的最大值单调栈，并从小到大枚举 $r$。记现在单调栈保存的下标为 $t_1,t_2,\cdots,t_k$，令 $t_0=0$，满足 $\forall i \in [1, k),b_{t_i}>b_{t_{i+1}}$。我们试图将 $r$ 压入栈中，考虑 $g_b(l,r-1)$ 怎样变化到 $g_b(l,r)$。当我们弹出 $t_i$ 时，显然有 $\forall l\in(t_{i-1},t_i],g_b(l,r-1)=b_{t_i},g_b(l,r)=b_r\Rightarrow g_b(l,r)-g_b(l,r-1)=b_r-b_{t_i}$。于是在弹出过程中，在线段树上对区间 $(t_{i-1},t_i]$ 中每个元素加上 $b_r-b_{t_i}$，即可维护 $r$ 时的 $g_b(l,r)$；自然，如果 $l$ 在弹出过程中未被波及，则 $g_b(l,r)=g(l,r-1)$。（最后单点更新 $g_b(r,r)=b_r$）

但我们要计算的是若干连续列的和。先利用前缀和简化：有 $f_b(p,i,j,q)=f_b(p,i,1,q)-f_b(p,i,1,j-1)$。$f_b(p,i,1,q)$ 即上述过程中线段树上区间 $[p,i]$ 内元素前 $q$ 轮的历史版本和。不妨考虑上述过程中每一次的增量在最终答案中的贡献。容易发现，如果在 $r$ 处执行了某次区间加操作，增量为 $\Delta$，且下标 $l$ 在该区间内，那么它对所有 $g_b(l,r’)\ \ (r’\geq r)$ 都有 $\Delta$ 的线性贡献，于是对 $f_b(p,i,1,q)\ \ (q\geq r,l\in[p,i])$ 的贡献为 $(q-r+1)\Delta={\color{blue}q\Delta}-{\color{red}(r-1)\Delta}$。易得位置 $l$ 在前 $r$ 轮累加的所有 $\Delta$ 就是 $g_a(l,r)$；而 $r,\Delta$ 只与区间加操作相关，$q$ 只与查询相关，故而我们开设另一棵线段树，维护所有 $-(r-1)\Delta$ 的区间和即可计算上述式子。

时间复杂度 $\bigO(Qn\log n)$。可以将上文中对每个询问构造的 $f_b$ 查询全部记录后，只执行一遍扫描线求出答案，最后统一回答，常数更小。

赛时代码（$\text{52 pts}$）

$\text{32 pts}$ – $a$ 是等概率随机生成的排列

CWOI 好像只有 hfy 赛场上写了该部分分。不过他的线段树被卡常了，怪出题人只给了 $\text{2s}$。

引理

在 $n!$ 个全排列中等概率随机选择一个排列 $p$，$p$ 所构建的笛卡尔树的树高期望是 $\bigO(\log n)$ 的。

证明

我们试图找到一个复杂度只跟 $a$ 强相关的算法，以充分利用这一性质。

不难发现，假如有 $\lbd(i)\geq \text{ql}\land \rbd(i)\leq \text{qr}$，那么我们总是可以直接累加 $a_if_b(\lbd(i),i,i,\rbd(i))$ 到答案中，不用考虑询问给定的限制。则我们可以用上文所述方法在 $\bigO(n\log n)$ 时间内求出 $a_if_b(\lbd(i),i,i,\rbd(i))\ \ (i=1,2,\cdots,n)$。

考虑在 $a$ 随机的情况下，有多少位置 $i$ 不能采用上式结果，而须考虑 $\text{ql},\text{qr}$ 的影响。显然，若 $a_{\text{mx}}=g_a(\text{ql},\text{qr})$，则位置 $\text{mx}$ 的答案可能要重新计算——必有 $\lbd(\text{mx})\leq \text{ql}\land \rbd(\text{mx})\geq \text{qr}$（否则和它是区间最值的条件相悖）。

考虑不断从区间最值位置向两侧迭代，也即 $$\newcommand\lmx{\operatorname{lmx}}\newcommand\rmx{\operatorname{rmx}}\begin{aligned}&\begin{cases}\lmx_k=\text{mx},& (k=0)\\a_{\lmx_k}=g_a(\text{ql},\lmx_{k-1}-1),& (\lmx_{k-1}>\text{ql})\\\lmx_k\text{\ is undefined}&\text{otherwise}\end{cases}\\&\begin{cases}\rmx_k=\text{mx},& (k=0)\\a_{\rmx_k}=g_a(\rmx_{k-1}+1,\text{qr}),& (\rmx_{k-1}<\text{qr})\\\rmx_k\ \text{is undefined}&\text{otherwise}\end{cases}\end{aligned}$$ 则不难说明有且仅有 $\lmx_k,\rmx_k\ \ (k=0,1,\cdots)$ 这些位置需要重新计算答案——其他所有位置 $i$ 的 $\lbd(i),\rbd(i)$ 最多延伸到（向左）$\lmx_k+1$ 或者（向右） $\rmx_k-1$，可以直接采纳预处理答案。

由于均有 $\lmx_k$ 是 $\lmx_{k-1}$ 在笛卡尔树上的子树元素（$\rmx$ 同理），且树高为 $\bigO(\log n)$ 的，故而暴力重算的复杂度得到保障。我们用 ST 表 找到 $\lmx_k$ 和 $\rmx_k$，将 $\bigO(Q\log n)$ 个询问挂载到对应右端点，最后统一做一遍上文所述的扫描线，复杂度为 $\bigO(Q\log^2 n+n\log n)$。

需要使用区间加区间求和树状数组优化常数才能通过，或者尝试用 $\bigO(\sqrt{n})$ 修改 $\bigO(1)$ 查询的块状数据结构平衡复杂度。（实际上本解法可以直接通过上一部分分。）

代码（$\text{84 pts}$）

正解（线段树）

当然了，我们有更简洁易写的分块做法。您可以移步别的题解。

我觉得出题人完全可以再给一组部分分：$\sum \text{qr}-\text{ql}+1\leq ?\times 10^5$。

设想矩阵 $\mathbf{F}$，满足 $\mathbf{F}_{i,j}=g_a(i,j)g_b(i,j)$。记 $$f(p,i,j,q)=\sum_{l=p}^{i}\sum_{r=j}^{q}\mathbf{F}_{l,r}=\sum_{l=p}^{i}\sum_{r=j}^{q}g_a(l,r)g_b(l,r)$$ 则题目所给询问，等价于问左上角为 $(\text{ql},\text{ql})$，右下角为 $(\text{qr},\text{qr})$ 的子矩阵元素之和。又因为可以认为有 $\forall l,r, n\geq l>r\geq 1,\mathbf{F}_{l,r}=0$，则我们把左上角变成 $(\text{ql},1)$，不影响结果。于是就变成了求 $f(\text{ql},\text{qr},1,\text{qr})$。

我们尝试对于 $r=1,2,\cdots,n$，直接维护每个 $l$ 的 $g_a(l,r)g_b(l,r)$，同时维护 $a,b$ 两序列的最大值单调栈。由于二者可能在第 $r$ 轮内先后更新，故为行文方便，下文中将用 $g_a(l)$ 直接代指目前线段树上维护的 $g_a(l,r)$，$g_a(l)’$ 则是相对于目前发生了改变的值；$g_b(l)$ 同理。

则在更新 $a$ 的单调栈时，在某个位置 $l$ 产生的增量 $\Delta_a=g_a(l)’-g_a(l)$ 将会导致 $l$ 的答案从 $g_a(l)g_b(l)$ 变成 $(g_a(l)+\Delta_a)g_b(l)$；更新 $b$ 的单调栈时同理。则若我们在线段树上每个节点维护子区间的 $g_a(l)$ 之和，$g_b(l)$ 之和以及 $g_a(l)g_b(l)$ 之和，现在每个位置产生增量 $\Delta_a,\Delta_b$，有 $$\begin{aligned} \sum_{l}g_a(l)’g_b(l)’&=\sum_{l}(g_a(l)+\Delta_a)(g_b(l)+\Delta_b)\\&=\left(\sum_{l}g_a(l)g_b(l)\right)+\left(\sum_{l}g_a(l)\right)\Delta_b+\left(\sum_{l}g_b(l)\right)\Delta_a+\sum_{l}\Delta_a\Delta_b\end{aligned}$$

$\Delta_a,\Delta_b$ 均导致线性贡献，显然满足结合律。于是用带 $\Delta_a,\Delta_b$ 延迟标记的线段树维护，就能在 $\bigO(\log n)$ 的时间内，在右端点扫描到 $r$ 时，查询 $g_a(l,r)g_b(l,r)$ 的区间和。

现在回顾部分分 $\bigO(n\log n)$ 处理单个查询的解法。我们分离了每一次的增量造成的贡献，并在最终线性累加回去。实际上对于上述更复杂的贡献，也能如法炮制：同样有 $f(p,i,1,q)$ 是线段树上的区间历史版本和。仍考虑 $g_a(l)g_b(l)$ 怎样变化到 $g_a(l)’g_b(l)’$。扫描到 $r$ 处更新 $a$ 的单调栈时，若在位置 $l$ 产生增量 $\Delta_a$，则对于 $q\geq r$ 的所有版本，$g_a(l,q)g_b(l,q)$ 都包含增量 $\Delta_ag_b(l)$。那么，对于某个查询 $f(p,i,1,q)\ \ (l\in[p,i],q\geq r)$，该次更新的增量造成的总贡献为 $\Delta_ag_b(l)(q-r+1)$，拆分成 ${\color{blue}\Delta_ag_b(l)}q-{\color{red}\Delta_a(r-1)g_b(l)}$。$b$ 的更新同理：${\color{blue}\Delta_bg_a(l)}q-{\color{red}\Delta_b(r-1)g_a(l)}$。

不难验证，对于一个确定的 $l$，在所有 $r\ \ (r\leq q)$ 处的两个蓝字部分贡献之和仍恰等于 $g_a(l,q)g_b(l,q)$，直接依照上文在线段树上维护区间和即可。现在着重考虑红字的求和。

我们尝试对于每个位置 $l$ 维护 $h(l)$，表示扫描线扫到 $r$ 时位置 $l$ 的红字贡献之和。

引理 $1$

对于一棵未采用标记永久化的线段树，某个叶子结点到根的路径上，未下放延迟标记的节点是以叶子为首的一个非空前缀。

引理 $2$

记上文中“只维护第 $r$ 轮的 $g_a(l,r)g_b(l,r)$ 区间和”线段树上，节点 $x$ 的延迟标记为 $\Delta_{a,x},\Delta_{b,x}$。设线段树上管辖 $g_a(l)g_b(l)$ 的叶子结点为 $x_1$，它和若干祖先构成的链为 $x_1,x_2,\cdots,x_k$，$x_k$ 为某次操作递归访问的终止节点（此即引理 $1$ 中的前缀）。则任一时刻，$g_a(l)$ 的真实值等于 $\sum_{i=1}^k\Delta_{a,x_i}$，而 $x_i$ 采用的“$g_a(l)$”实际上是 $\sum_{j=1}^{i}\Delta_{a,x_j}$；$g_b(l)$ 之于 $\Delta_{b,x}$ 亦然。

这两条引理都是很容易验证的。

考虑怎样维护 $h(l)$ 的区间和。假若扫描线扫描到第 $r$ 轮，我们更新了 $b$ 的单调栈，使得一段区间的 $h(l)’=h(l)+\Delta_b(r-1)g_a(l)$。则将当前 $g_a(l)$ 的值记作 $c_a$，它的贡献仍然是线性的：访问线段树某一节点时，由于其所有祖先的延迟标记都已下放，我们获得的正是 $g_a(l)$ 的真实值。故可以立刻更新节点 $x_k$ 的 $$\sum_{l}h(l)’=\left(\sum_{l}h(l)\right)+\Delta_b(r-1)\sum_{l}g_a(l)$$

此后该区间可能经过了若干次更新，维护的 $g_a(l)$ 和 $\Delta_{a,x}$ 可能发生变化，但那一次修改所采用的的 $c_a$ 是不变的（参见上图）。为了保证下放后 $h(l)$ 增量的一致性，我们将 $c_a$ 拆分成 ${\color{red}\Delta_{a,x_k}}+{\color{blue}\sum_{i=1}^{k-1}\Delta_{a,x_i}}$，$h(l)$ 的增量变成 $$c_a\Delta_b(r-1)={\color{red}\Delta_{a,x_k}}\Delta_b(r-1)+{\color{blue}\sum_{i=1}^{k-1}\Delta_{a,x_i}}\Delta_b(r-1)$$

如上图所示，蓝字就是 $x_{k-1}$ 所维护的“$g_a(l)$”，它在把标记 $\Delta_{a,x_k}$ 下放到 $x_{k-1}$ 前保持不变，我们将其加以利用。故而下放时，依次作如下更新：令延迟标记 $\Delta_{\beta,x}$ 为应用到 $x$ 上且还未下放的 $\Delta_b(r-1)$ 之和（$\Delta_{\alpha,x}$ 是 $\Delta_a(r-1)$ 之和）；有 $x_{k-1}$ 维护的 $$\sum_{l}h(l)’=\left(\sum_{l}h(l)\right)+\Delta_{\beta,x_k}\left(\sum_l{\color{blue}g_a(l)}\right)+\Delta_{\alpha,x_k}\left(\sum_l{g_b(l)}\right)$$ （$\sum_lg_a(l),\sum_lg_b(l)$ 暂未更新）；对于红字，我们在对 $x_k$ 作修改时即立刻保存 $\Delta_b(r-1){\color{red}\Delta_{a,x_k}}$，将其累加到另一延迟标记中，记作 $\Delta_{\text{co},x_k}$；下放时即有 $$\sum_{l}h(l)’=\left(\sum_{l}h(l)\right)+\left(\sum_{l}\Delta_{\text{co},x_k}\right)$$ （注意到红字累加的是常系数，与来自于对 $a$ 还是对 $b$ 的修改无关，故而 $a$ 的修改共用 $\Delta_{\text{co},x_k}$）

$\Delta_{\beta,x_k},\Delta_{\alpha,x_k}$ 的下放更新是简单的，将它直接累加到 $\Delta_{\beta,x_{k-1}},\Delta_{\alpha,x_{k-1}}$ 上即可；而 $\Delta_{\text{co},x_k}$ 下放时，由上图可得有 $${\Delta_{\text{co},x_{k-1}}}’=\Delta_{a,x_{k-1}}\Delta_{\beta,x_k}+\Delta_{b,x_{k-1}}\Delta_{\alpha,x_k}+\Delta_{\text{co},x_k}$$

这些更新完成后，再行处理 $\sum_{l}g_a(l),\sum_{l}g_b(l)$ 和 $\sum_{l}g_a(l)g_b(l)$ 的更新。于是我们对每个节点 $x$ 维护九元组 $(\sum_{l}g_a(l),\sum_{l}g_b(l),\sum_{l}g_a(l)g_b(l),\sum_{l}h(l),\Delta_{a,x},\Delta_{b,x},\Delta_{\alpha,x},\Delta_{\beta,x},\Delta_{\text{co},x})$。题目所给每个询问 $[\text{ql},\text{qr}]$，都只需在扫到第 $\text{qr}$ 轮时区间查询 $\sum_{l=\text{ql}}^{\text{qr}}\text{qr}g_a(l)g_b(l)-h(l)$。

时间复杂度 $\bigO(Q\log n+n\log n)$，常数大。

R96818778 记录详情

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
#include <bits/stdc++.h>
using namespace std;

#define inl inline
// 快读已省略。
#define newl putchar('\n')
typedef long long ll;
typedef unsigned long long ull;
typedef pair <int, int> pint;
#define fst first
#define scd second
#define all(p) begin (p), end (p)
#define empb emplace_back

constexpr int N = 250010;
int _test, n, m, l, r, a[N], b[N]; ull ans[N];
int sta[N], topa, stb[N], topb;
vector <pint> q[N];

struct seg_tree {
	struct info { ull da, db, dalp, dbta, dco; };
	struct node { ull l, r, gasum, gbsum, gagbsum, hsum; info tag; } t[N<<2];
	info inc; ull idx, L, R;

	void build (int x, int l, int r) {
		t[x].l = l, t[x].r = r;
		if (l == r) return;
		int mid = l + r >> 1;
		build (x<<1, l, mid),
		build (x<<1|1, mid + 1, r);
	}
	inl void saku (node &nde, const info &tag) {
		static ull len; len = nde.r - nde.l + 1;
		info &_tag = nde.tag;
		const auto &[da, db, dalp, dbta, dco] = tag;
		nde.hsum += dalp * nde.gbsum + dbta * nde.gasum + dco * len;
		nde.gasum += da * len, nde.gbsum += db * len;
		nde.gagbsum += da * db * len + db * nde.gasum + da * nde.gbsum;
		_tag.dco += dco + _tag.db * dalp + _tag.da * dbta;
		_tag.da += da, _tag.db += db,
		_tag.dalp += dalp, _tag.dbta += dbta;
	}
	inl void down (int x) {
		saku (t[x<<1], t[x].tag),
		saku (t[x<<1|1], t[x].tag),
		memset (&t[x].tag, 0, 40);
	}
	inl void post (int x) {
		node &nde = t[x], &ls = t[x<<1], &rs = t[x<<1|1];
		nde.gasum = ls.gasum + rs.gasum,
		nde.gbsum = ls.gbsum + rs.gbsum,
		nde.gagbsum = ls.gagbsum + rs.gagbsum,
		nde.hsum = ls.hsum + rs.hsum;
	}
	
	void add (int x) {
		if (t[x].l >= L && t[x].r <= R)
			return saku (t[x], inc);
		ull mid = t[x].l + t[x].r >> 1; down (x);
		if (L <= mid) add (x<<1);
		if (R > mid) add (x<<1|1);
		post (x);
	}
	inl void add (int l, int r, ull da, ull db, ull idx) {
		inc = { da, db, (1ull-idx)*da, (1ull-idx)*db,
			(da&&db) * (1ull-idx)*da*db } /* 特判对r的单点更新，此时由于da,db同时更新要增加额外系数 */;
		L = l, R = r, add (1);
	}
	ull query (int x) {
		if (t[x].l >= L && t[x].r <= R)
			return t[x].gagbsum * idx + t[x].hsum;
		ull mid = t[x].l + t[x].r >> 1;
		down (x); ull res = 0;
		if (L <= mid) res += query (x<<1);
		if (R > mid) res += query (x<<1|1);
		return res;
	}
	inl ull query (int l, int r, int _idx) {
		return L = l, R = r, idx = _idx, query (1);
	}
} seg;

int main () {
	/* NOIP 2022 SC-067 吴秋实 */
	// freopen ("match.in", "r", stdin);
	// freopen ("match.out", "w", stdout);

	read (_test, n);
	for (int i = 1; i <= n; ++i) read (a[i]);
	for (int i = 1; i <= n; ++i) read (b[i]);
	seg.build (1, 1, n);
	read (m);
	for (int i = 1; i <= m; ++i)
		read (l, r), q[r].empb (l, i);
	for (int r = 1; r <= n; ++r) {
		static int dt;
		// 更新单调栈。
		while (topa && (dt = a[r] - a[sta[topa]]) > 0)
			seg.add (sta[topa-1]+1, sta[topa], dt, 0, r), --topa;
		while (topb && (dt = b[r] - b[stb[topb]]) > 0)
			seg.add (stb[topb-1]+1, stb[topb], 0, dt, r), --topb;
		seg.add (r, r, a[r], b[r], r);
		sta[++topa] = stb[++topb] = r;
		for (const auto [l, id] : q[r])
			ans[id] = seg.query (l, r, r);
	}
	for (int i = 1; i <= m; ++i)
		print (ans[i]), newl;

	return 0;
}