CF1747E – List Generation – 题解

这道破题拖了我整整一天。

代数推导

转化为容斥模型

题目所给限制可以表述为，$a$ 和 $b$ 均为单调不降的序列，长度相等（记为 $k$），且 $a_1=0,a_k=n,b_1=0,b_k=m,\nexists i\in[2,k],a_i=a_{i-1}\land b_i=b_{i-1}$。

考虑差分序列 ${a_i}’=a_i-a_{i-1}\quad(i\in[2,k])$，${b_i}’$ 同理，它与原序列形成双射。于是不存在 ${a_i}’={b_i}’=0$ 的差分序列合法。考虑 $\sum_{i=2}^{k}{a_i}’=n$，也就是和为 $n$ 的 $k-1$ 元线性方程组的一组非负整数解；$b’$ 同理。容易计算“钦定至少有 $c$ 个位置不合法”的方案数——利用容斥原理即可得到长为 $k$ 的合法序列对个数为 $$\sum_{c=0}^{k-2}\binom{k-1}{c}\binom{n+(k-1)-1-c}{(k-1)-1-c}\binom{m+(k-1)-1-c}{(k-1)-1-c}(-1)^c$$ 答案累加上式结果 $\times k$。

恒等变换

$$\begin{aligned} \text{答案}&=\sum_{k=2}^{n+m+1}k\sum_{c=0}^{k-2}\binom{k-1}{k-1-c}\binom{n+k-2-c}{k-2-c}\binom{m+k-2-c}{k-2-c}(-1)^c\\ &=\sum_{k=2}^{n+m+1}k\sum_{c=0}^{k-2}\binom{k-1}{c+1}\binom{n+c}{c}\binom{m+c}{c}(-1)^{k-2-c}&\text{（倒序求和）}\\ &=\sum_{c=0}^{n+m-1}\binom{n+c}{c}\binom{m+c}{c}(-1)^c\sum_{k=c+2}^{n+m+1}(-1)^kk\binom{k-1}{c+1}\\ &=\sum_{c=0}^{n+m-1}\binom{n+c}{c}\binom{m+c}{c}(-1)^c\sum_{k=c+2}^{n+m+1}(-1)^k\frac{k!}{(c+1)!(k-c-2)!}\\ &=\sum_{c=0}^{n+m-1}\binom{n+c}{c}\binom{m+c}{c}(-1)^c(c+2)\sum_{k=c+2}^{n+m+1}(-1)^k\binom{k}{c+2}\\ \end{aligned}$$

递推转移

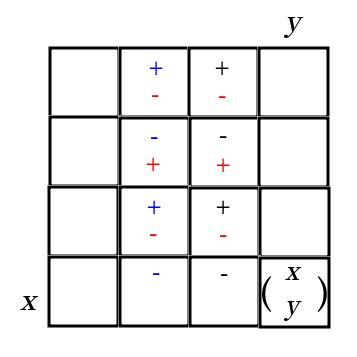
二项式系数矩阵。黑字表示 $h(c+1)$ 之系数，红字表示 $h(c+1)$ 的等价系数（由递推公式得），蓝字为 $h(c)$ 之系数。

记 $h(c)=\sum_{k=c}^{n+m+1}(-1)^k\binom{k}{c}$。我们难以找到简便的通项公式。尝试将其二项式系数拆分后递推计算。有 $$\begin{aligned} h(c+1)&=\sum_{k=c+1}^{n+m+1}\binom{k}{c+1}(-1)^k\\ &=-\sum_{k=c}^{n+m}\binom{k+1}{c+1}(-1)^k\\ &=-\sum_{k=c}^{n+m}\left({\color{red}\binom{k}{c+1}}+{\color{blue}\binom{k}{c}}\right)(-1)^k\\ &=-\left({\color{red}h(c+1)-\binom{n+m+1}{c+1}(-1)^{n+m+1}}+{\color{blue}h(c)-\binom{n+m+1}{c}(-1)^{n+m+1}}\right) \end{aligned}$$ 移项整理得到 $$h(c)=\binom{n+m+2}{c+1}(-1)^{n+m+1}-2h(c+1)$$ 故而答案为 $$\sum_{c=0}^{n+m-1}\binom{n+c}{c}\binom{m+c}{c}(-1)^c(c+2)h(c+2)$$

时间复杂度 $\operatorname{O}(n+m)$，组合数应当预处理到 $2(n+m)$ 级别。

Bonus: 无意义过程

记 $$\begin{aligned} &w_{k,c}=\binom{n+k-2-c}{k-2-c}\binom{m+k-2-c}{k-2-c}(-1)^c\\&f(k,\Delta)=\sum_{c=0}^{k-2}\binom{k-1}{c+\Delta}w_{k,c} \end{aligned}$$ 经过与上文相仿的推导可以发现，有 $$f(k,\Delta)=w_{k,0}\binom{k-1}{\Delta}-f(k-1,\Delta)-f(k-1,\Delta+1)$$。我们的目标是分别求出 $k=2,\cdots,n+m+1$ 的 $f(k,0)$。考察每一个 $w_{k_0,0}\binom{k_0-1}{\Delta_0}$ 对 $f(k,0)\quad(k\geq k_0)$ 的贡献。上式除首项以外，递推形式与二项式系数相同（本来就是通过对原式拆系数得到的），因此 $w_{k_0,0}\binom{k_0-1}{\Delta_0}$ 以 $(-1)^{k-k_0}\binom{k-k_0}{\Delta_0}$ 的系数贡献到 $f(k,0)$ 中。

于是考察单个系数对答案的最终贡献。有 $w_{k_0,0}$ 的贡献为 $$\begin{aligned} &w_{k_0,0}\sum_{\Delta_0=0}^{k_0-1}\binom{k_0-1}{\Delta_0}\sum_{k=k_0}^{n+m+1}\binom{k-k_0}{\Delta_0}(-1)^{k-k_0}k\\ =&w_{k_0,0}\sum_{k=k_0}^{n+m+1}\left(\sum_{\Delta_0=0}^{k_0-1}\binom{k_0-1}{\Delta_0}\binom{k-k_0}{\Delta_0}\right)(-1)^{k-k_0}k\\ =&w_{k_0,0}\sum_{k=k_0}^{n+m+1}\binom{k-1}{k_0-1}(-1)^{k-k_0}k&\href{https://oi-wiki.org/math/combinatorics/vandermonde-convolution/#推论-4-及证明}{（范德蒙德卷积）} \end{aligned}$$

然后就殊途同归了。

组合意义

解一 – 构造标识符数组

解二 – 网格图合法路径关键点计数