FHQ Treap 学习笔记

UPD 02.15：更新了区间操作部分。

约莫半月前练习专题时，发现几道解法多样的题目，其中需要运用一些中高级数据结构。苦于之前没有学习过平衡树，便挑选了一种易于上手、实现简单的平衡树学习，也即FHQ Treap。由11年国家队队员范浩强发明。

为书写方便，文章中可能将直接使用$p$代指某节点的随机权值，$\text{val}$代指节点关键码（即记录的数值），$h$代指树高，$\text{siz}$代指子树大小，$\text{cnt}$代指节点副本数（相同关键码的节点），$\text{rt}$存储根节点编号。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
mt19937 rnd (time (0));
struct treap {
	int tot, rt;
	struct node {
		int val, lson, rson, cnt, siz;
		unsigned long prio;
	} t[N];
	
	inl int load (int val) {
		t[++tot] = { val, 0, 0, 1, 1, rnd () };
		return tot; }
	#define post(x) (t[x].siz = t[t[x].lson].siz + t[t[x].rson].siz + t[x].cnt)
	// ...
}

0x00 关于Treap

“Treap”是”tree”和”heap”的合成词，意即“带有堆性质的二叉查找树”。怎么个“堆性质”法呢？我们知道，在一个序列上建立的二叉查找树是不唯一的。考虑下面这张图：

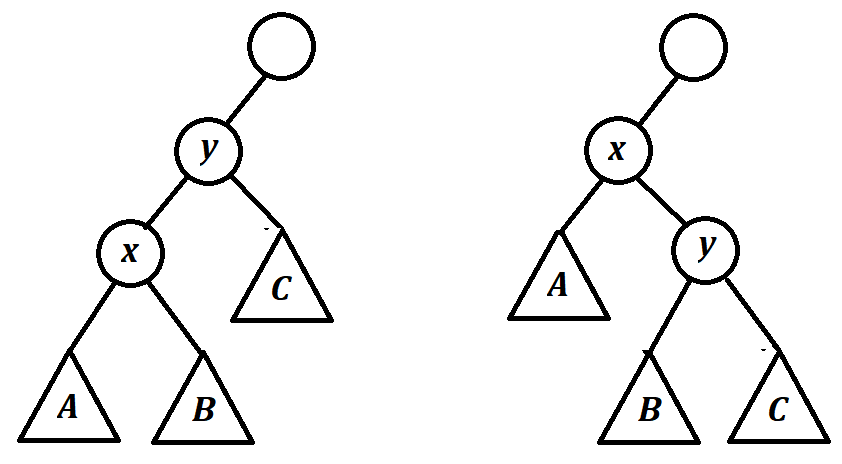
这张图或许会对下一节的理解有帮助。这两个子树的$x$和$y$节点位置对调，但都满足$A \leq x \leq y$，$x<B\leq y$，$C > y > x$。同时，该序列的中序遍历不改变（均为${A, x, B, y, C}$），这一性质在区间操作时非常关键。也就是说，我们考虑在维护二叉查找树的BST性质时，为每一个节点分配一随机权值$p$，同时以某种方法维护随机权值的堆性质。这样一来，Treap的期望高度是$\mathrm{O}(\log n)$的（证明请参考这里）。

维护的一种方式是旋转，也就是在对节点进行操作时检查其权值$p_x$与父亲节点$p_{fa}$的关系，若不满足大根堆/小根堆性质，则将其照上图所示旋转。而另一种方式——直接对满足一定要求的两棵子树按权值合并——则不需要旋转，这就是FHQ Treap的精妙之处。

0x10 核心操作

FHQ Treap只有两种核心操作：分裂与合并。因此它也被称作”分裂合并Treap”。

0x11 分裂

分裂操作旨在将一棵Treap分裂成两棵，使得其中一棵（$A$）的所有节点的关键码$\text{val}$不大于$\text{key}$，而另一棵（$B$）的关键码大于$\text{key}$。或者，使得树$A$的节点数量恰为$\text{siz}$，其存储的是原树中排名不超过$\text{siz}$的节点，而$B$反之。我们先讨论前一种分裂。

split函数是一个递归的过程，它并非一调用就明白“哪些节点应该属于树$A$，哪些不属于”，而需要在原树上作二分查找。考虑现在正分裂节点$x$及其子树。若$\text{val}_x \leq \text{key}$，说明$x$及其左子树应当全部属于$A$，而其右子树中应存在部分节点$y$，其$\text{val}_y \leq \text{key}$，所以我们向右子树递归分裂。反之，若$\text{val}_x >\text{key}$，则其右子树全部属于$B$，我们向左子树递归分裂。

考虑前一种情况。假定现在我们对$x$的右子树的分裂已经完成，得到两棵树$A’$和$B’$。容易发现，由于$A’$中所有节点在原右子树上，则其关键码一定大于$x$，这时我们直接将$A’$作为$x$的右子树，$x$的左子树不变，而$x$成为新的$A$的根节点，并令$B’$为树$B$即可。递归应用这个过程，即可将整棵树按$\text{key}$划分成$A \leq \text{key} < B$。时间复杂度$\mathrm{O}(h)$。

如果要下放延迟标记/更新子树信息（如子树大小），则应分别在分裂递归的前后完成。

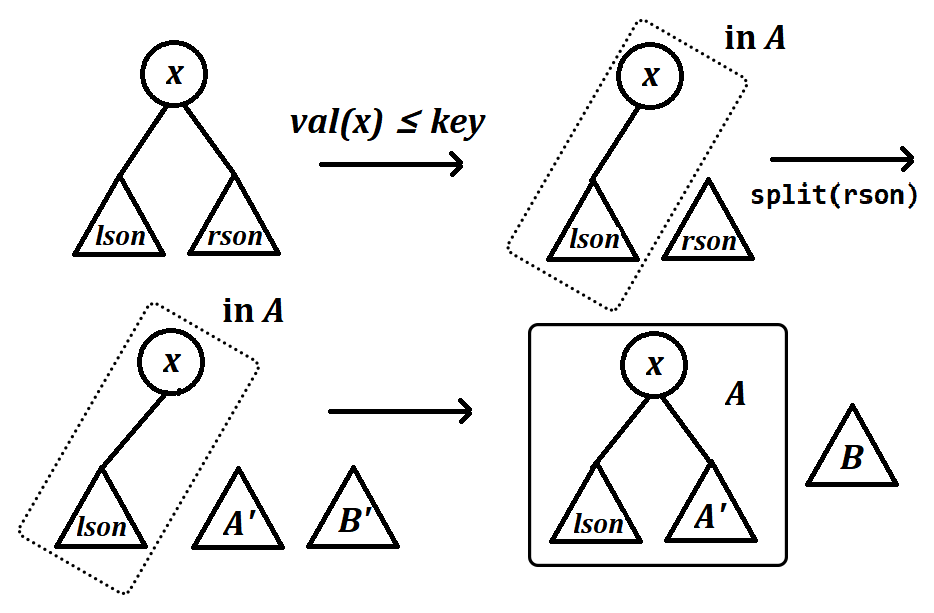
代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
pair <int, int> split (int x, int key) {
	if (!x) return { 0, 0 }; // 两棵空树
	pair <int, int> o;
	if (t[x].val <= key) {
		o = split (t[x].rson, key); // o = { 树A', 树B' }
		t[x].rson = o.first; // 令A'为x的右儿子
		post (x); // 更新子树信息
		return { x, o.second }; // { 树A, 树B }
	} else {
		o = split (t[x].lson, key);
		t[x].lson = o.second; // 令B'为x的左儿子
		post (x); // 更新子树信息
		return { o.first, x };
	}
}

若要按照子树大小分裂，类比按照关键码分裂的思路即可。参见区间操作一节。

0x12 合并

合并操作将两棵Treap $A$与$B$合并在一起，要满足$\forall x \space \text{in} \space A, y \space \text{in} \space B, \text{val}_x \leq \text{val}_y$，即树$A$不大于树$B$。

由于两棵树已经相对有序，所以我们能够借助BST形态的不唯一性，维护其堆性质。考虑两个节点$x \space \text{in} \space A, y \space \text{in} \space B$，则我们既可以让$x$及其子树作为$y$的左子树的一部分存在，又可以让$y$及其子树作为$x$的右子树的一部分存在。同时，为维护大根堆/小根堆性质，我们选择$x$与$y$中$p$更大/更小的一棵作为根即可。随后我们递归合并“$x$与$y$的左子树”或者“$x$的右子树与$y$”即可。时间复杂度$\mathrm{O}(h)$。

1
2
3
4
5
6
7
8
9
10
11
int merge (int x, int y) {
	if (!x) return y;
	if (!y) return x;
	if (t[x].prio >= t[y].prio) {
		t[x].rson = merge (t[x].rson, y);
		post (x); return x;
	} else {
		t[y].lson = merge (x, t[y].lson);
		post (y); return y;
	}
}

0x20 基本运用

0x21 插入节点

插入一个关键码为$\text{val}$的节点。我们将整棵树分为不大于/大于$\text{val}$的两棵树$A, B$，将$A$分为小于/等于$\text{val}$的两棵树$A’, x$。若$x$非空（已存在相同关键码的节点），则直接增加其副本数和子树大小；否则新建节点。合并$A’, x$作$A$，合并$A, B$。时间复杂度$\mathrm{O}(h)$。

听说为了实现方便，主流写法是“即使可能已存在相同关键码的节点，也直接插入一个新的节点”，并不记录副本数等。但这样会造成一定效率问题。以下写法旨在提高插入效率和减少节点数。

1
2
3
4
5
6
7
8
9
10
int load (int val) {
	t[++tot] = { val, 0, 0, 1, 1, rnd () };
	return tot; }
void insert (int val) {
	pair <int, int> o = split (rt, val),
		p = split (o.first, val - 1);
	if (!p.second) p.second = load (val);
	else ++t[p.second].cnt, ++t[p.second].siz;
	rt = merge (merge (p.first, p.second), o.second);
}

0x22 删除节点

和插入节点类似，我们将整棵树分为关键码不大于/大于$\text{val}$的树$A, B$，再将$A$分为小于/等于$\text{val}$的两棵树$A’, x$，此时节点$x$就是我们应当删除/减少副本数的节点。视情况考虑是否将$A’$和$x$合并，然后将$A$与$B$合并即可。时间复杂度$\mathrm{O}(h)$。

1
2
3
4
5
6
void del (int val) {
	pair <int, int> o = split (rt, val), p = split (o.first, val - 1);
	if (--t[p.second].cnt, --t[p.second].siz) // 若副本数大于1
		p.first = merge (p.first, p.second);
	rt = merge (p.first, o.second);
}

0x23 查询$\text{val}$的排名

直接将整棵树按小于/大于等于$\text{val}$划分为树$A, B$，查询$A$的大小$+1$即可。时间复杂度$\mathrm{O}(h)$。当然，为了更出色的效率，也可以应用普通BST的递归查找过程：在树上查找$\text{val}$，对于每一次向$x$右子树的递归，将答案累加$x$的左子树的$\text{siz}$以及$x$的副本数。

1
2
3
4
5
6
7
8
9
10
11
12
int rank (int x, int val) {
	pair <int, int> o = split (rt, val - 1);
	int res = t[o.first].siz + 1;
	return rt = merge (o.first, o.second), res;
}

/* 普通BST查找写法 */
int rank (int x, int val) {
	if (t[x].val == val) return t[t[x].lson].siz + 1;
	return t[x].val > val ? rank (t[x].lson, val)
		: rank (t[x].rson, val) + t[x].cnt + t[t[x].lson].siz;
}

0x24 查找排名为$k$的数

提供普通BST的查找写法：若$k$不大于左子树大小，则答案在左子树中；若$k$不超过该节点副本数与左子树大小之和，则答案在该节点；否则，答案在右子树中。在右子树中查找的就应是排名为$k$减去前二者之和的数。若有其他FHQ Treap特有的写法，欢迎在页底提出。时间复杂度$\mathrm{O}(h)$。

1
2
3
4
5
6
int kth (int x, int rk) {
	if (!x) throw "kth not found.";
	if (t[t[x].lson].siz >= rk) return kth (t[x].lson, rk);
	if (t[x].cnt + t[t[x].lson].siz >= rk) return t[x].val;
	return kth (t[x].rson, rk - t[x].cnt - t[t[x].lson].siz);
}

0x25 查询$\text{val}$的前驱

亦有两种写法。既可以利用其特性，将树分为小于/大于等于$\text{val}$的两棵树$A, B$，然后在$A$中查找排名为$A$的大小的数；也可以应用普通BST的查找：查找$\text{val}$，对于每一个经过的节点，尝试更新$\text{val}$的最大前驱。若找到$\text{val}$，则考虑在节点$x$的左子树中最靠右（$\text{val}$最大）的节点。复杂度依然为$\mathrm{O}(h)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int precu (int val) {
	pair <int, int> o = split (rt, val - 1);
	int res = kth (o.first, t[o.first].siz);
	return rt = merge (o.first, o.second), res;
}

/* 普通BST查找写法 */
int precu (int val) {
	int res = -INF, x = rt;
	while (x) {
		if (t[x].val == val) {
			if (x = t[x].lson) {
				while (t[x].rson) x = t[x].rson;
				res = t[x].val;
			}
			break;
		}
		if (t[x].val < val) res = max (res, t[x].val);
		x = t[x].val < val ? t[x].rson : t[x].lson;
	}
	return res;
}

0x26 查询$\text{val}$的后继

同理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int succe (int val) {
	pair <int, int> o = split (rt, val);
	int res = kth (o.second, 1);
	return rt = merge (o.first, o.second), res;
}

/* 普通BST查找写法 */
int succe (int val) {
	int res = INF, x = rt;
	while (x) {
		if (t[x].val == val) {
			if (x = t[x].rson) {
				while (t[x].lson) x = t[x].lson;
				res = t[x].val;
			}
			break;
		}
		if (t[x].val > val) res = min (res, t[x].val);
		x = t[x].val < val ? t[x].rson : t[x].lson;
	}
	return res;
}

洛谷题库 P3369 【模板】普通平衡树 的 AC代码

0x30 区间操作

（二月十五日更新）

引入“区间树”的概念：每一个节点维护的是一段连续的区间。人见人爱的线段树就是最通用的区间树之一，能够将一段区间剖分成$\log_2(n)$级别的子区间后进行各种操作。

平衡树也可以维护序列。我们知道，二叉搜索树的中序遍历就是将所有元素从小到大排序后的有序序列。插入某个元素，也就等价于向原有序序列中的对应位置插入该元素。同时，既然如此，如果我们将序列位置视作元素，那么也就等价于维护序列了。对于一个节点$x$，它所维护的区间，就是其子树上排名最小的节点到排名最大的节点，也就是从$x$一直分别向左子树和右子树访问到达的节点。

Splay、AVL、FHQ Treap等平衡树广泛支持各种区间操作。FHQ Treap的一大特色，就在于可以将整个区间直接从树上分裂出来，再行操作，相对来说更加直观。

分裂、合并的过程是否会破坏原序列的顺序？对于一棵树的中序遍历序列中的两个元素$x, y$，$x$先于$y$出现，则$x$在$\text{lca}(x, y)$的左子树中，$y$在右子树中（或作为$x$的祖先存在）。若它们在新的序列中交换了位置，当且仅当左右子树交换了位置。考虑分裂的过程，发现没有发生任何两元素相对位置改变的情况；对于合并，由于我们保证$A$中所有元素小于$B$（对应在序列上，也就是$A$代表的子段先于$B$对应子段出现），则为保持这一性质，$A$中所有元素之间相对位置不改变，$B$亦然；而考虑$x \in A$，$y \in B$，则在合并完成的BST中，必然有$x$处于$\text{lca}(x, y)$的左子树中，$y$位于其右子树中。故分裂合并操作不会改变原序列每两个元素间的相对位置。

为了保证时间复杂度，需要延迟标记以避免不合时宜的更新。标记和维护的信息种类繁多，但它们的作用可以归结为一句话：

没有必要的事情就不做，必要的事情尽快完成。

什么意思呢？也就是说，我们需要保证，在任何时刻访问某一节点，或者在其子树结构发生改变之前，其维护的区间信息一定是完备的、已更新完成的。而对于没有访问的节点，我们不去理会。可以类比线段树的$\text{lazytag}$。

仍然考虑分裂和合并操作。假如分裂了$x$的子树，则$x$维护的区间确实发生了改变，所以我们下放其标记。以分裂了$x$的右子树为例。则$x$的左子树维护的区间保持不变；右子树中，一旦在节点$y$处发生一次分裂，则$y$的左子树将和树$A$合并，其维护的区间不改变。以此类推，只要我们保证在分裂前后及时更新子树/父亲节点的信息，就不会出现任何问题。

下面将结合例题[NOI2005] 维护数列，给出一些经典区间操作的实现。

本题中需要维护区间和、区间最大连续子段和，支持区间翻转、区间覆盖、插入区间、删除区间操作。上传信息、下传标记时维护区间和、区间元素、区间左右侧最大连续子段和、区间翻转位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
mt19937 rnd (time (0));
struct treap {
	struct node {
		int lson, rson, siz, sum, val, lmax, rmax, sgmx;
		unsigned int prio;
		bool rev, rep; int tag;
	} t[G], *ls, *rs;

	int rt, idx, qu[N], l, r;  // 内存循环回收利用。
	int st[N], top, c[N];
	treap () {
		for (int i = 1; i <= G; ++i) qu[i] = i;
		l = 1, r = G; }
	int load (int val) {
		idx = qu[l = l % G + 1];
		t[idx] = { 0, 0, 1, val, val, val, val,
			val, rnd (), 0, 0, 0 };
		return idx; }
	void upd_mx (int x) { // 在区间内元素统一时，更新区间最大子段和相关信息。
		t[x].lmax = t[x].rmax = t[x].sgmx = (t[x].val >= 0 ? t[x].siz : 1) * t[x].val; }
	void post (int x) {
		ls = &t[t[x].lson], rs = &t[t[x].rson]; // 减少不连续内存访问
		t[x].siz = ls->siz + rs->siz + 1;
		t[x].sum = ls->sum + rs->sum + t[x].val;
		// 更新最大连续子段和。
		t[x].lmax = max (ls->lmax, ls->sum + t[x].val + max (0, rs->lmax));
		t[x].rmax = max (rs->rmax, rs->sum + t[x].val + max (0, ls->rmax));
		t[x].sgmx = max (max (ls->sgmx, rs->sgmx), t[x].val + max (rs->lmax, 0) + max (ls->rmax, 0));
	}
	void down (int x) {
		ls = &t[t[x].lson], rs = &t[t[x].rson];
		if (t[x].rev) {
			swap (t[x].lson, t[x].rson); swap (ls, rs);
			ls->rev ^= 1, rs->rev ^= 1;
			t[x].rev = 0;
			// 最大连续子段和翻转。 
			swap (ls->lmax, ls->rmax),
			swap (rs->lmax, rs->rmax);
		}
		if (t[x].rep) {
			int &tag = t[x].tag;
			ls->rep = rs->rep = 1;
			ls->sum = ls->siz * tag, rs->sum = rs->siz * tag;
			ls->val = rs->val = ls->tag = rs->tag = tag;
			upd_mx (t[x].lson), upd_mx (t[x].rson);
			t[x].rep = tag = 0;
		}
	}

	pair <int, int> split (int x, int lmt) {
		if (!x) return { 0, 0 };
		pair <int, int> o; down (x);
		if (t[t[x].lson].siz + 1 <= lmt) {
			o = split (t[x].rson, lmt - t[t[x].lson].siz - 1);
			t[x].rson = o.first; post (x);
			return { x, o.second };
		} else {
			o = split (t[x].lson, lmt);
			t[x].lson = o.second; post (x);
			return { o.first, x };
		}
	}
	int merge (int x, int y) {
		if (!x || !y) return x | y;
		if (t[x].prio >= t[y].prio) {
			down (x);
			t[x].rson = merge (t[x].rson, y);
			return post (x), x;
		} else {
			down (y);
			t[y].lson = merge (x, t[y].lson);
			return post (y), y;
		}
	}
	
	// ...
}

0x31 区间分裂并插入若干元素

参见上述代码中的split函数。

具体来讲，若我们要在$\text{pos}$后插入若干元素，则可以将整棵树以“排名不大于$\text{pos}$”划分成$A, B$。构建一棵由待插入元素构成的序列树$C$。观察到Treap是笛卡尔树，我们应用笛卡尔树的$\mathrm{O}(n)$建树方法，免去暴力操作的麻烦。将$A,C$合并，$A,B$合并即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void dfs (int x) {
	if (!x) return;
	dfs (t[x].lson); dfs (t[x].rson);
	post (x);
}
void insert (int pos, int len) {
	// 在pos后插入len个元素，元素暂存在c数组。
	// 单调栈O(n)建立笛卡尔树。
	pair <int, int> o = split (rt, pos);
	int id, _top; top = 0;
	for (int i = 1; i <= len; ++i) {
		id = load (c[i]); _top = top;
		while (_top && t[st[_top]].prio < t[id].prio) --_top;
		if (_top) t[st[_top]].rson = id;
		if (_top < top) t[id].lson = st[_top + 1];
		st[top = _top + 1] = id;
	}
	dfs (st[1]); // 通过DFS自底向上更新信息。
	rt = merge (merge (o.first, st[1]), o.second);
}

0x32 删除若干元素

直接将该区间剖分出来，合并序列前缀和后缀即可。由于这道题内存吃紧，采用了内存回收机制。

1
2
3
4
5
6
7
8
9
10
11
#define SPLIT pair <int, int> o = split (rt, pos - 1), p = split (o.second, len)
#define MERGE rt = merge (o.first, merge (p.first, p.second))
void recyc (int x) {
	if (!x) return;
	qu[r = r % G + 1] = x;
	recyc (t[x].lson); recyc (t[x].rson);
}
void del (int pos, int len) {
	SPLIT; recyc (p.first);
	rt = merge (o.first, p.second);
}

0x33 区间覆盖

将该区间剖分出来，在区间树的根节点打上repl标记（区间覆盖），更新区间和以及区间最大子段和相关信息后合并。

1
2
3
4
5
6
void replace (int pos, int len) {
	SPLIT; int &x = p.first;
	t[x].sum = len * c[0], t[x].rep = 1,
	t[x].tag = t[x].val = c[0];
	upd_mx (x); MERGE;
}

0x34 区间翻转

考虑区间翻转的本质：区间中每两个元素相对位置互换。对应到二叉树的中序遍历上，也就是这棵树的每个节点的左右儿子调换。因此我们保存reve标记（是否需要翻转子区间），将该区间剖分出来后其标记异或$1$再行合并。

1
2
3
4
void rever (int pos, int len) {
	SPLIT; t[p.first].rev ^= 1;
	swap (t[p.first].lmax, t[p.first].rmax);
	MERGE; }

0x35 查询区间和

如题，剖分出该区间并查询其子树和即可。

1
2
3
4
int query (int pos, int len) {
	SPLIT; int res = t[p.first].sum;
	return MERGE, res;
}

0x36 查询序列最大连续子段和

个人感觉这是本题最难的部分。

蓝书上有一道经典例题，使用线段树维护区间最大连续子段和，支持单点修改。对于静态序列，可以使用线性复杂度的DP解决；否则一般采取分治。具体来讲，对于区间$[l, r]$，我们将其拆分成$[l, \text{mid}], (\text{mid}, r]$。考虑它最大连续子段和的来源：紧靠左端点的某个区间$[l, \text{pos}]$，紧靠右端点的某个区间$[\text{pos}, r]$，以及横贯两子区间的$[\text{pos}_1, \text{pos}_2],\text{pos}_1 \in [l, mid], \text{pos}_2 \in (mid, r]$。它们都可以通过利用左右子区间的信息拼凑计算。详情参阅本节开头的post函数以及upd_mx函数。

还需要注意在区间翻转时应交换该节点的左右侧最大子段和；区间覆盖时应当直接贪心地更新三者的数据……细节繁多。查询时只需要根节点的数据。

洛谷题库 P2042 [NOI2005] 维护序列 的 AC代码

0x40 可持久化

待更。