随记 – 二月四日 – 将树形结构序列化的几种办法

DFS序列（$\mathrm{dfn}$）

在没有或存在一定限制条件的情况下，以DFS遍历经过的节点顺序构成的序列。记$\mathrm{dfn}(x)$为第一次访问该节点的时间戳，$\mathrm{seq}(t)$为访问序为$t$的节点。

容易发现，节点$x$的子树节点的$\mathrm{dfn}$一定是一段连续的区间。故我们可以使用数据结构方便地维护子树的信息。

欧拉序

和DFS序不同，欧拉序在每个节点开始/结束访问时均会被记录一次，故该序列的长度为$2n$，$n$为节点数。例如，对于下面这棵树，一个合法的欧拉序是${0, 2, 3, 3, 4, 1, 1, 4, 2, 0}$。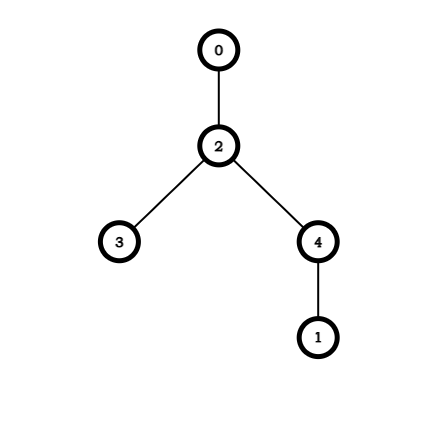

记序列为$\mathrm{seq}$，每个节点开始访问的时间戳为$\mathrm{st}(x)$，结束访问的时间戳为$\mathrm{ed}(x)$，有$\mathrm{seq}(\mathrm{st}(x))=\mathrm{seq}(\mathrm{ed}(x))=x$。则$\mathrm{st}(4)=5$，$\mathrm{ed}(4)=8$。

欧拉序可以处理路径上的问题。考虑$x \leftrightarrow y$的简单路径，它可以被看做欧拉序上连续的一段。我们取序列中的这些元素：

$$\mathrm{seq}(t), t \in \begin{cases}[\mathrm{st}(x), \mathrm{st}(y)], & \text{当}x\text{和}y\text{存在“祖先 – 儿子”关系}，\text{且设}x\text{是}y\text{的父亲}\\ [\mathrm{ed}(x), \mathrm{st}(y)], & \text{其他情况，并令}\mathrm{st}(x)<\mathrm{st}(y) \end{cases}$$

若同一个节点在该区间中出现了$2$次，说明在$x \leftrightarrow y$的简单路径上不存在该节点，不统计其信息，否则作统计。还需要注意，当$x, y$互不为祖先时，其$\mathrm{lca}$不会出现在子区间中（参看欧拉序的定义），需要额外统计。

它往往与根号分治、分块、莫队等算法有机结合，处理树上路径的询问。[WC2013] 糖果公园是其经典应用。

树链剖分

点击小标题出门右转OI Wiki。