CF1624D – Finding Zero – 题解与思路重现

给大家表演一个一场下青

CodeForces Round 770 Div.2 Problem D – Finding Zero

一道非常有意思的交互和构造题。

考虑能否固定两个数$x, y$，通过它们的相对大小关系，确定其他数中是否存在$0$或最大值$a_{\text{max}}$。

经过一番推导，我们发现，设$x \geq y$的情况下，对于三元组$(a_i=x, a_j=y, a_k=z)$，有$$g(i, j, k)\newline
=\max(a_i, a_j, a_k) – \min(a_i, a_j, a_k)=
\begin{cases}z-y, & z > x \\
x-y, & z \in [y, x]\\
x-z, & z < y\end{cases}$$。所以，设$x=6, y=4$以上式结果为因变量，$z$为自变量，应有以下图像：

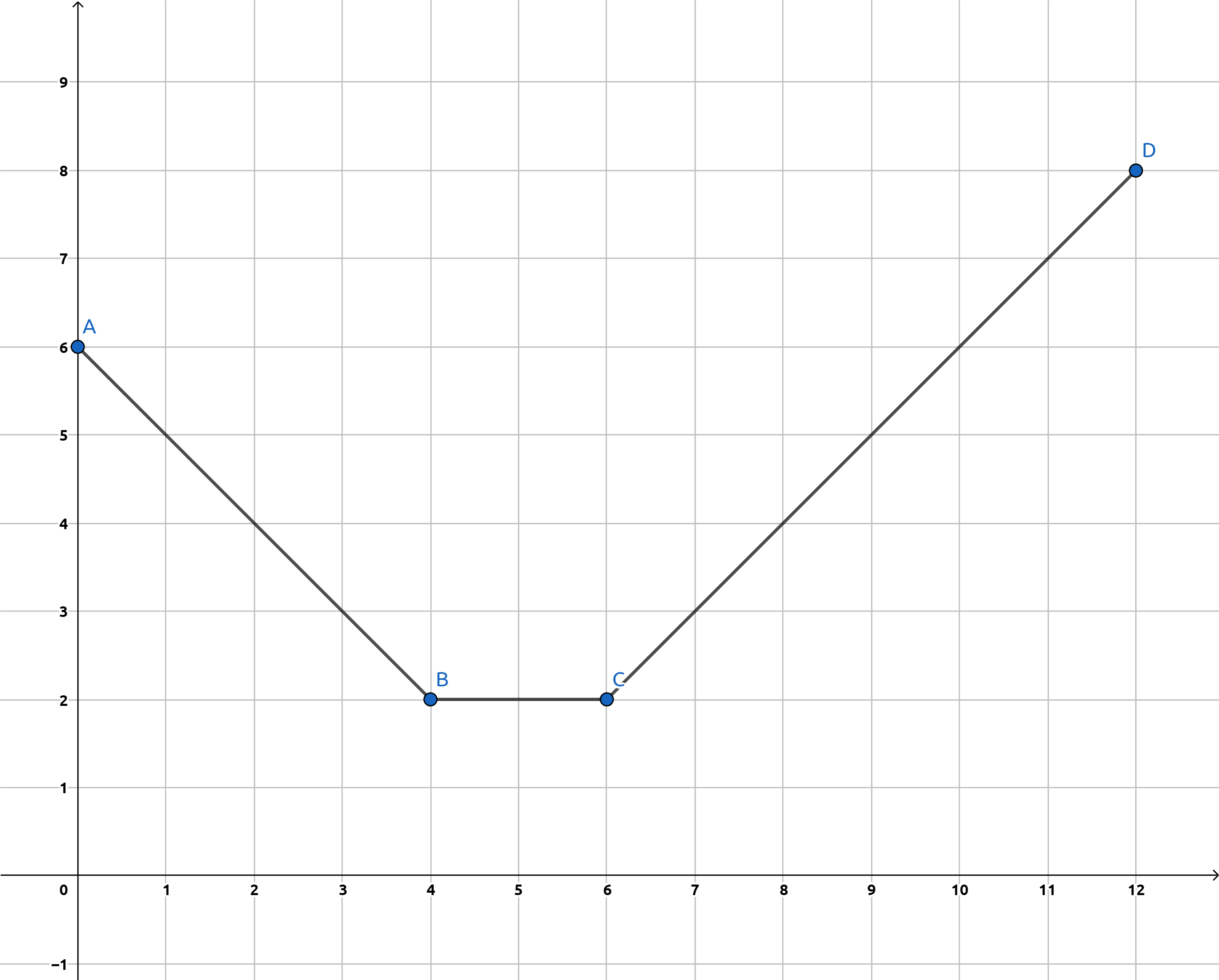
容易发现，在给定的$a$序列当中取$z$，当$g$取到最大值时，$z$为$0$或者$a_{\text{max}}$。令$x=\max(a_1, a_2), y=\min(a_1, a_2)$。现在我们就已经知道了数列中其中一个最值的位置。那么，如何判别这是$a_{\text{max}}$还是$0$呢？

设该最值的位置为$p$。容易发现，不论$a_p$是$a_{\text{max}}$还是$0$，设$q$为另一个最值的位置，则有$\max(a_i, a_j, a_p) – \min(a_i, a_j, a_p), p \neq i, p\neq j$在$j=q$或$i=q$时取到最大值，否则与题设和定义相矛盾。同时，由于题目要求输出至多两个可能存在$0$的位置，我们需要更准确地判定另一个最值的位置。则我们枚举$i$，令$j=i \mod n+1$，计算$g(i, j, p)$，则由于$g(q-1, q, p)$和$g(q, q+1, p)$两个结果均会取到最大值，故我们可以由此确定$q$的位置。这时答案就是$(p, q)$。

还有一个比较棘手的问题：当$\forall i, j, 3 \leq i < j \leq n, g(1, 2, i)=g(1, 2, j)$怎么办？一开始（赛时）我采取分类讨论的想法，发现出现这种情况，只可能是因为

1. $x, y$中既包含$a_{\text{max}}$又包含$0$（下图粉红色点集）；
2. $x, y$中包含$0$，且$\forall i \in [3, n], a_i=a_{\text{max}}$（下图绿色点集）；
3. $x, y$中不包含$0$，但$\forall i \in [3, n], (a_i>x \wedge a_i-y=\text{constant})\vee(a_i<y \wedge x-a_i=\text{constant})$（下图浅蓝色点集）。

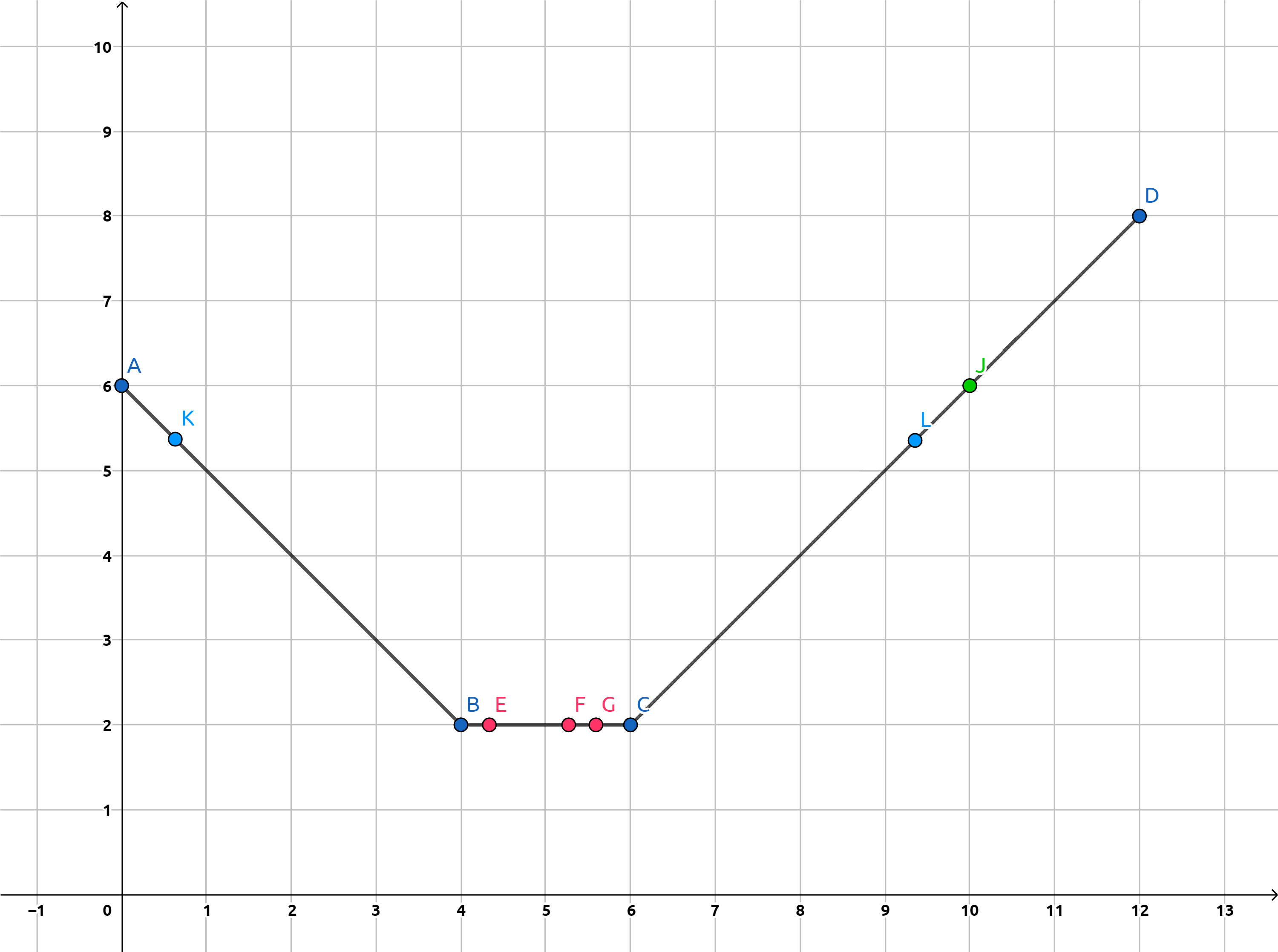
为什么不包含“$x$是$a_{\text{max}}$，$y\neq 0$”的情况？因为这样一来，由题意可得$a_3=a_4=\dots=a_n=0$，与题设相矛盾。

再来考虑有什么办法能够将这三种情况统一起来。最开始，我考虑选出$x, y, z, c$，分别计算$g(x, y, c), g(x, z, c), g(y, z, c)$，然后取$g$的最小值，认为其补集就是最值所在位置（例如，若$g(x, z, c)$取到最小，则$y$是最值）。但这种方法在第三种情况会出问题。

但今天我发现，这三种情况有一个共性：最大值和最小值紧挨在一起，即$|p-q|=1$或$|p-q|=n-1$。第一种情况无需证明；对于情况二，无论$a_1=0$还是$a_2=0$，都有$a_n=a_{\text{max}}=a_3$；第三种情况，容易证明$\forall i \in [3, n], a_i = a_{\text{max}} \vee a_i=0$。所以，我们直接计算所有三元组$g(i, i \mod n + 1, (i + 1)\mod n+1), i \in [1, n]$，找到$g$的最大值，和上述一种情况一样选择产生$g_p=g_{p+1}=g_{\text{max}}$的$p$，计算$p$和$p+1$代表的三元组的交集即可。

总体来看，对于情况A，我们使用了$(n-2)+(n-1)=2n-3$次询问；情况B则采用了恰好$2n-2$次询问。

实现时应当注意各种细节。Submission #145491065

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
#include <bits/stdc++.h>
using namespace std;

template <typename T> inline bool read (T &x) {
	x = 0; int f = 1; char c = getchar ();
	for (; c != EOF && !isdigit (c); c = getchar ())
		if (c == '-') f = -1;
	if (c == EOF) return 0;
	for (; c != EOF && isdigit (c); c = getchar ())
		x = (x<<1) + (x<<3) + (c^48);
	x *= f; return 1;
}
template <typename T, typename... Targs>
inline bool read (T &x, Targs&... args) {
	return read (x) && read (args...); }
template <typename T> void print (T x) {
	if (x < 0) putchar ('-'), x = -x;
	if (x > 9) print (x / 10);
	putchar ('0' + x % 10);
}
template <typename T, typename... Targs>
inline void print (T x, Targs... args) {
	print (x), putchar (' '), print (args...); }
#define reint register int
#define inl inline
#define newl putchar('\n')
typedef long long ll;
typedef unsigned long long ull;
// typedef __int128 lll;
typedef pair <int, int> pint;

constexpr int N = 1024;
int T, n, keko[N], pos[N][2], mx, mxfr;
bool f, out; int tot;

inl int publ (int a[2], int b[2]) {
	int g[4] = { a[0], a[1], b[0], b[1] };
	sort (g, g + 4);
	for (int i = 1; i < 4; ++i)
		if (g[i] == g[i - 1]) return g[i];
}
inl int ask (int i, int j, int k) {
	printf ("? %d %d %d\n", i, j, k);
	fflush (stdout);
	int res; scanf ("%d", &res);
	return fflush (stdout), res;
}
#define outp(x, y) (printf ("! %d %d\n", x, y), fflush (stdout))
#define proc(x) ((((x) - 1) + n) % n + 1)

int main () {
	/* CF1634D Finding Zero 吴秋实 */
read (T);
while (T--) {
	read (n); f = 1; mx = -1; out = tot = 0;
	for (int i = 3; i <= n; ++i)
		keko[i] = ask (1, 2, i);
	for (int i = 3; i <= n; ++i) {
		if (i > 3 && keko[i - 1] != keko[i]) f = 0;
		if (keko[i] > mx)
			mxfr = i, mx = keko[i];
	}

	if (f) {
		for (int i = 1; i <= n - 2; ++i)
			keko[i] = ask (i, i + 1, i + 2);
		keko[n - 1] = ask (n - 1, n, 1);
		keko[n] = ask (n, 1, 2);
		mx = -1;
		for (int i = 1; i <= n; ++i)
			mx = max (mx, keko[i]);
		for (int i = 1; i <= n; ++i)
			if (keko[i] == mx && keko[proc (i + 1)] == mx) {
				outp (proc (i + 1), proc (i + 2));
				out = 1; break;
			}
		if (!out) outp (1, 2);
		continue;
	}
	for (int i = 1; i <= n; ++i) {
		if (i == mxfr) continue;
		++tot;
		if (i == proc (mxfr - 1))
			pos[tot][0] = i, pos[tot][1] = proc (mxfr + 1);
		else pos[tot][0] = i, pos[tot][1] = proc (i + 1);
		keko[tot] = ask (mxfr, pos[tot][0], pos[tot][1]);
	}
	mx = -1;
	for (int i = 1; i <= tot; ++i)
		mx = max (mx, keko[i]);
	for (int i = 1; i <= tot; ++i) {
		int pre = i - 1 ? i - 1 : tot;
		if (keko[i] == mx && keko[pre] == mx) {
			outp (mxfr, publ (pos[i], pos[pre]));
			out = 1; break;
		}
	}
	if (!out) outp (1, 2);
}

	return 0;
}