OI

CF1017G – The Tree – 题解与思路重现

CodeForces Round #502 Problem G – The Tree

这是lty数据结构专题里唯二自己做出来的题目中的一道。

如果不包含“将 xx 的子树全部染白”的操作，应当怎样处理？

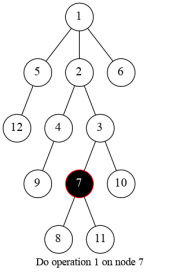
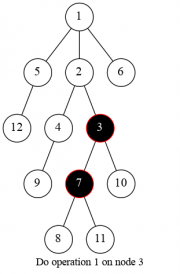
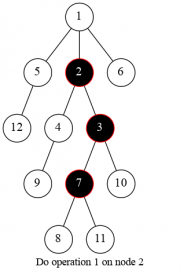
题目所给操作可以这样转述：令 xx 为本次染色操作的节点。若 xx 为白色，则立刻染黑并退出；否则我们找到其子树中的，与 xx 相连的黑色连通块，则对于每个连通块底部节点，若其不是叶子节点，我们将其儿子染黑。

由于本题的树没有特殊性质，且将来加入回退操作，故而难以维护整个连通块以及其叶子节点。因此，我们可以从“在何种情况下，节点 xx 被染黑”的方向考虑。

显然，只有从在 xx 到根的路径上的节点开始的染色操作，才可能波及到 xx。假如最终 xx 被染黑的一瞬，它被包含在了以 comprt\text{comprt} 为根的连通块中。令链 ⟨comprt,x⟩\langle\text{comprt}, x\rangle 为 {x1,x2,…,xn},x1=comprt,xn=x\left\{x_1,x_2,\dots,x_n \right\},x_1=\text{comprt},x_n=x，那么自然想到，一种一定合法的染色序列是 {y1,y2,⋯ ,yn}\{y_1,y_2,\cdots,y_n\}，其中有 ∀k∈[1,n]∩Z,yk∈{x1,⋯ ,xk}\forall k \in [1, n] \cap \mathbb{Z},y_k \in \{x_1,\cdots,x_k\}，也即我们每一步都在该连通块内部，并将连通块的最大深度推进一层。

这种序列确实合法（它是充分条件），但这真的是 xx 被染黑的必要条件么？

我们发现，不论在第 kk 轮染色的节点为 yky_k 是否包含在以 comprt\text{comprt} 为根的“目标连通块”中，它总是能够将 ⟨comprt,x⟩\langle \text{comprt}, x\rangle 被染黑的节点层数推进一层。因为本题的操作保证递归的染色一定不会在黑色节点终止，故而总有一层白色节点变黑。就算在某次染色后，上下两个连通块发生合并，则下次染色在合并后的大连通块任意位置进行，都将涉及到下层连通块的儿子节点。那么，当 ⟨comprt,x⟩\langle \text{comprt}, x\rangle 所有层都被染黑时，xn=xx_n=x 自然也无路可逃了。正因如此，我们实际上根本不关心每一次染色的位置。则我们立刻得出以下结论：

令 ⟨rt,x⟩={x1=rt,x2,⋯ ,xn=x}\langle \text{rt}, x\rangle=\{x_1=\text{rt},x_2,\cdots,x_n=x\} 是 xx 到根的祖先后代链。令 pre⁡x(k)=∑i=1k[xiis colored black]\operatorname{pre}_x(k)=\sum_{i=1}^{k}[x_i \text{is colored black}]（染黑节点数的前缀和），则 xx 被染黑的充分必要条件是 ∃k∈[0,n)∩Z,pre⁡x(n)−pre⁡x(k)≥n−k\exists k \in [0,n) \cap \mathbb{Z}, \operatorname{pre}_x(n)-\operatorname{pre}_x(k)\geq n-k。

该式是一个树上根到某节点路径的前缀和统计。我们不妨转写其为 pre⁡x(n)−n≥pre⁡x(k)−k\operatorname{pre}_x(n)-n\geq \operatorname{pre}_x(k)-k，使其两侧均只分别与 n,kn, k 相关，易于查询和维护。故而我们通过线段树结合重链剖分维护（对于每个节点 yy 而言）pre⁡y(dep⁡(y))−dep⁡(y)\operatorname{pre}_y(\operatorname{dep}(y))-\operatorname{dep}(y)，在染色时对子树所有节点加上 11，查询 xx 是否为黑色时考虑到根的路径上该式的最小值，将之与 pre⁡x(dep⁡(x))−dep⁡(x)\operatorname{pre}_x(\operatorname{dep}(x))-\operatorname{dep}(x) 比较即可。

现在加入子树清空操作。假如我们现将 xx 及其子树全部赋为白色，则

  • 子树内部进行的所有操作失效；
  • 在祖先后代链 ⟨rt,x⟩\langle \text{rt},x\rangle 进行的部分操作失效。

也即，根据上文提到的操作序列的性质，我们确有可能在 ⟨rt,x⟩\langle \text{rt},x\rangle 上染色，使得连通块扩展到 xx 的子树内。但现在该连通块最多只能够扩展到 fa⁡(x)\operatorname{fa}(x)。如果仍为扩展到 xx，则以下的调整均可以忽略；否则，是否要一一按顺序找出这些操作，然后尽数删除它们造成的贡献么？显然不行，其它子树内部的由这些操作产生的贡献仍然需要保留。故而我们尝试以等价方式调整 xx 及其子树的前缀和，使其满足 ∀k∈[0,dep⁡(x)),pre⁡x(dep⁡(x))−dep⁡(x)<pre⁡x(k)−k\forall k \in [0, \operatorname{dep}(x)), \operatorname{pre}_x(\operatorname{dep}(x))-\operatorname{dep}(x)<\operatorname{pre}_x(k)-k。

那我们直接把 pre⁡x(dep⁡(x))\operatorname{pre}_x(\operatorname{dep}(x)) 调整为 min⁡{pre⁡x(k)−k∣k∈(0,dep⁡(x)}−1\min\{\operatorname{pre}_x(k)-k\mid k \in (0, \operatorname{dep}(x)\}-1 就行了？

事实证明，这样做是正确的。考虑该调整是否与之前的条件契合：xx 子树以外的数据没有受到改变，若其先前自洽，则调整后仍自洽；对于 xx 子树内节点，由于内部操作被清空，必然有 ∀y∈subtree rooted at x,pre⁡y(dep⁡(y))=pre⁡x(dep⁡(x))\forall y \in \text{subtree rooted at }x, \operatorname{pre}_y(\operatorname{dep}(y))=\operatorname{pre}_x(\operatorname{dep}(x))，而在计算 xx 是否染黑时，只利用该式子的相对大小关系，而非利用不等号左右两侧式子之差作精确统计，同时 xx 祖先们的染色操作造成的联通块层数扩张仍将如实反映到各个子树中；对于将来在子树内部的操作，其相对大小关系显然仍是自洽的。故而该调整的正确性得到保障。

综上所述，我们通过数据结构维护上述式子的区间（链上）最值，在染色时区间自增，在查询颜色时考虑区间最小值，在清空子树时区间赋值（此处应注意，须赋调整后的 pre⁡x(dep⁡(x))\operatorname{pre}_x(\operatorname{dep}(x)) 而非其加上 −dep⁡(x)-\operatorname{dep}(x)），就完成了本题。

时间复杂度 O(nlog⁡2n)\mathrm{O}(n \log^2 n)。

Submission #164125980

  1. 1
  2. 2
  3. 3
  4. 4
  5. 5
  6. 6
  7. 7
  8. 8
  9. 9
  10. 10
  11. 11
  12. 12
  13. 13
  14. 14
  15. 15
  16. 16
  17. 17
  18. 18
  19. 19
  20. 20
  21. 21
  22. 22
  23. 23
  24. 24
  25. 25
  26. 26
  27. 27
  28. 28
  29. 29
  30. 30
  31. 31
  32. 32
  33. 33
  34. 34
  35. 35
  36. 36
  37. 37
  38. 38
  39. 39
  40. 40
  41. 41
  42. 42
  43. 43
  44. 44
  45. 45
  46. 46
  47. 47
  48. 48
  49. 49
  50. 50
  51. 51
  52. 52
  53. 53
  54. 54
  55. 55
  56. 56
  57. 57
  58. 58
  59. 59
  60. 60
  61. 61
  62. 62
  63. 63
  64. 64
  65. 65
  66. 66
  67. 67
  68. 68
  69. 69
  70. 70
  71. 71
  72. 72
  73. 73
  74. 74
  75. 75
  76. 76
  77. 77
  78. 78
  79. 79
  80. 80
  81. 81
  82. 82
  83. 83
  84. 84
  85. 85
  86. 86
  87. 87
  88. 88
  89. 89
  90. 90
  91. 91
  92. 92
  93. 93
  94. 94
  95. 95
  96. 96
  97. 97
  98. 98
  99. 99
  100. 100
  101. 101
  102. 102
  103. 103
  104. 104
  105. 105
  106. 106
  107. 107
  108. 108
  109. 109
  110. 110
  111. 111
  112. 112
  113. 113
  114. 114
  115. 115
  116. 116
  117. 117
  118. 118
  119. 119
  120. 120
  121. 121
  122. 122
  123. 123
  124. 124
  125. 125
  126. 126
  127. 127
  128. 128
  129. 129
#include <bits/stdc++.h>
using namespace std;

/* 快读已省略。 */

#define inl inline
#define reint register int
#define newl putchar('\n')
typedef long long ll;
// typedef unsigned long long ull;
// typedef __int128 lll;
// typedef long double llf;
typedef pair <int, int> pint;
#define fst first
#define scd second
#define all(p) begin (p), end (p)

constexpr int N = 1e5 + 10, INF = 0x3f3f3f3f;
int n, m, x, y, ope, siz[N], dep[N], fa[N];
int top[N], dfn[N], owa[N], dtot, hson[N], seq[N];
vector <int> e[N];

void dfs (int x) {
	dep[x] = dep[fa[x]] + 1,
	siz[x] = 1, hson[x] = 0;
	for (const int y : e[x]) {
		dfs (y), siz[x] += siz[y];
		if (siz[hson[x]] < siz[y])
			hson[x] = y;
	}
}
void decomp (int x, int tp) {
	dfn[x] = ++dtot, top[x] = tp;
	seq[dtot] = x;
	if (!hson[x]) { owa[x] = dtot; return; }
	decomp (hson[x], tp);
	for (const int y : e[x])
		if (y != hson[x]) decomp (y, y);
	owa[x] = dtot;
}

inl void gomn (int &x, int y) { x = min (x, y); }
struct seg_tree {
	struct node { int l, r, stag, dtag, mxdep, mn; } t[N<<2];

	#define post(x) (t[x].mn = min (t[x<<1].mn, t[x<<1|1].mn))
	void build (int x, int l, int r) {
		t[x] = { l, r, INF, 0, 0, 0 };
		if (l == r) { t[x].mn =
			-(t[x].mxdep = dep[seq[l]]); return; }
		int mid = l + r >> 1;
		build (x<<1, l, mid);
		build (x<<1|1, mid + 1, r);
		post (x); t[x].mxdep = max
			(t[x<<1].mxdep, t[x<<1|1].mxdep);
	}
	inl void _set (int x, int num) {
		t[x].mn = num - t[x].mxdep,
		t[x].stag = num, t[x].dtag = 0; }
	inl void _inc (int x, int dt) {
		t[x].mn += dt, t[x].dtag += dt; }
	inl void down (int x) {
		int &stag = t[x].stag, &dtag = t[x].dtag;
		if (stag != INF) {
			_set (x<<1, stag), _set (x<<1|1, stag);
			stag = INF; }
		_inc (x<<1, dtag), _inc (x<<1|1, dtag);
		dtag = 0;
	}

	#define FUNCTION(name, inn)\
	void name (int x, int L, int R, int num) {\
		if (t[x].l >= L && t[x].r <= R)\
			return inn (x, num); \
		int mid = t[x].l + t[x].r >> 1; down (x);\
		if (L <= mid) name (x<<1, L, R, num);\
		if (R > mid) name (x<<1|1, L, R, num);\
		post (x);\
	}
	FUNCTION (cover, _set);
	FUNCTION (add, _inc);
	int query (int x, int L, int R) {
		if (t[x].l >= L && t[x].r <= R) return t[x].mn;
		int mid = t[x].l + t[x].r >> 1;
		int res = INF; down (x);
		if (L <= mid) gomn (res, query (x<<1, L, R));
		if (R > mid) gomn (res, query (x<<1|1, L, R));
		return res;
	}
} seg;

inl void cover (int x) {
	int mn = min (-1, seg.query (1,
		dfn[x], dfn[x])), y = fa[x];
	while (y) gomn (mn, seg.query
		(1, dfn[top[y]], dfn[y])-1), y = fa[top[y]];
	seg.cover (1, dfn[x], owa[x], mn += dep[x]);
}
inl bool query (int x) {
	int mn = 0, y = fa[x];
	while (y) gomn (mn, seg.query
		(1, dfn[top[y]], dfn[y])), y = fa[top[y]];
	return seg.query (1, dfn[x], dfn[x]) >= mn;
}

int main () {
	/* CF1017G. The Tree 吴秋实 */
	#ifdef LOCAL
	freopen ("CF1017G.in", "r", stdin);
	freopen ("CF1017G.out", "w", stdout);
	#endif
	
	read (n, m);
	for (y = 2; y <= n; ++y)
		read (x), fa[y] = x, e[x].push_back (y);
	dfs (1), decomp (1, 1);
	seg.build (1, 1, n);
	for (int i = 1; i <= m; ++i) {
		read (ope, x);
		switch (ope) {
			case 1: seg.add (1, dfn[x], owa[x], 1); break;
			case 2: cover (x); break;
			case 3: puts (query (x) ? "black" : "white"); break;
		}
	}

	return 0;
}
  • 2022年7月16日

Tags:

You may also like...

发表回复

您的电子邮箱地址不会被公开。 必填项已用 * 标注

成都外国语学校高二 OIer。喜欢搞些杂七杂八的小项目。常去骑车。复健中，脚力已不如前。

一言(ひとこと)

暫し空に祈りて 愛を断て

分类目录