终于体会到了“看了题解都可能写不出来”的绝望了——CF925E May Holidays。
自以为已经对“分块”的思想有了一定掌握,到头来发现自己还只会最基本的、应用最广泛的值域分块。只是题见得不够多罢了。
考虑一种实际操作中不会使用的求区间第大的算法。设块长为,我们将序列分成块,每一块内直接对元素排序。对于一个询问,我们二分答案。猜测答案为,在中间的每一整块内二分出的元素数量,两侧暴力查找。这样的复杂度是的,其中代表区间长。
这告诉我们,分块的目的不仅可以让较大的值域范围内的统计变得更高效,还可以使得元素(部分)有序,适用范围更加广泛。就连分块这种暴力数据结构使用时都需灵活变通,其他算法又何尝不是如此。
这道题的题意让我们想起了最小循环节。我们先不考虑这个矩阵的具体位置。由题可知,只要扩展的矩阵覆盖原矩阵即可。考虑以下图形:
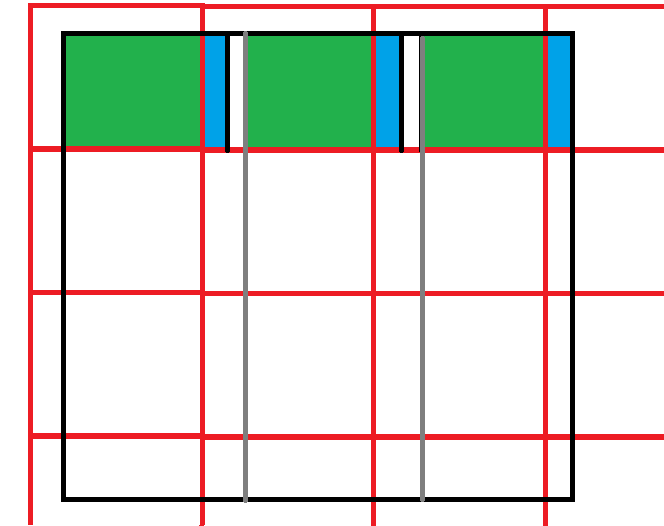
黑线为原矩阵。红线是一种最小子矩阵的划分。请看绿色和蓝色矩形,它们分别是没有占够一整个矩形宽度的左右边界,以及对应到每个完整的子矩形中的位置。如果我们以灰线为界,将最小子矩形平移至与灰线之间对齐,则最小子矩形的扩展就从原矩形的最左端开始。上下两端的处理同理。这与之前的划分显然是等价的。因此,我们可以只考虑从左端、顶端开始的子矩阵的划分。
又是一道明明很明晰却困了我一个上午的题。完了我刷蓝书的进度要被吊打了
解一 字符串Hash结合二分
预处理出两个字符串的前缀哈希。对于每一个的后缀,设其与的最大匹配长度为。容易发现二者前缀哈希是否相等具有单调性。二分每个后缀的答案,最后统计每种的计数即可。代码实现略。
其实昨晚扫一眼题就想到了这个做法。要不是愣是要研究KMP,也不至于沦落到如此地步(
解二 KMP模式匹配与next数组
说来惭愧。从国庆到现在,至少有3个人试图把我讲懂期望,但我还是只明白最基本的定义,根本不会做题。
今天发现一篇入门级别的数学期望讲解,在此转载。